In previous posts I said that the extent to which "Fund people" works will depend on the distribution of scientific talent. Think about the following situation: Imagine that only a handful of scientists at every point in time are able to –if given the time and means–lead revolutions on par with the work of Darwin, Einstein, or Galileo (This is an extreme case admittedly because most of science does not look like this; most of science is more incremental and less memorable). I recently found two authors that believe something like this,

Braben, whose book Scientific Freedom I reviewed says that even though most scientists could be the next Einstein if they tried, only a few will even try:

It is possible that my message may be seen as elitist and of interest only to those very few scientists who might be putative members of a twenty - first century Planck Club. That interpretation would be wrong. One of the themes here is that almost every serious researcher is at some time in a career capable of taking those fateful steps that might lead to a great discovery or the creation of penetrating new insight. They might then need to draw on vast reserves of courage and determination, and perhaps also a little luck if they are to make progress. At any one time, of course, the proportion of researchers ready to seize that possibly once - in - a - lifetime opportunity will be very small, so if they are prevented from doing so the democratic pressure they can exert is insignifican't. [...] a properly constituted TR initiative should appeal to only a small number of scientists with radical thoughts on their minds. The challenge is to recognize them as there are millions of scientists, and one does not even know which haystack hides the needle. [...] Let us assume that there were about 300 transformative researchers — the extended membership of the Planck Club — during the twentieth century.

In physics, Lee Smolin is even more on the elitist side, with even fewer scientists in the revolutionaries' club:

“But when it comes to theoretical physics, we are not talking about much money at all. Suppose that an agency or foundation decided to fully support all the visionaries who ignore the mainstream and follow their own ambitious programs to solve the problems of quantum gravity and quantum theory. We are talking about perhaps two dozen theorists. Supporting them fully would take a tiny fraction of any large nation’s budget for physics.”

I think there is something to this view, and it is not incompatible with what I said in my last blogpost (That peer review can select the best work). In physics, there has been no progress in the fundamentals of the field since the 70s, so one could argue that perhaps there are key assumptions that need to be thrown away, that there is a strong need for funding what to many physicists seem obviously wrong. In that case peer review may be stifling progress: physics could benefit from less clever math and more philosophical thought, going back to the mode of thinking of Einstein et al. as Smolin suggests. Braben does not oppose peer review in general, he argues that peer review will systematically underrate those coming up with paradigm-breaking ideas, and most of science is not that.

In biology, in contrast with physics, whatever the current framework is (if any)¹ , it continues to be extremely fruitful. If one takes CRISPR, which has been arguably been a case of "good science", one can break it down into:

1. Noticing that there are suspicious repetitive sequences in certain bacteria

2. Figuring out what those are for

3. Leveraging them into a tool for gene editing

4. Further improving CRISPR (e.g. Prime Editing)

None of these examples of good science (Or perhaps engineering if you count the last 2) are paradigm shifts but without any doubt CRISPR has been highly useful and influential, both in academia, and soon in the clinic.

In wikipedia, only a small fraction (10%) of the active users do most (90%) of the edits. Is science like this, or even more extreme? Ioannidis et al. (2014) note there are 15M scientists that published anything in the 1996-2011 period, but only 1% that has published every single year in this period. This smaller 150k-strong group accounts for 40% of all papers and 87% of all papers with >1000 citations.

Nobel Prize winner William Shockley published (1957) a paper measuring the distribution of productivity in an already high-performing environment: the Los Alamos Scientific Laboratory as well as the Brookhaven National Laboratory. Shockley finds a log-normally distribution of publications and patents: Most scientists publish very little and a progressively smaller count publish increasingly more.

There's the observation of Lotka's law (Yes, it's the same Lotka as in Lotka-Volterra) that says that the relative frequency of authors with a given number of publications follows a power law that scales with the square of the number of articles published; for example out of 100 scientists who publishes at least 1 article, only 1 will publish 10 articles. The precise exponent may vary by discipline (Pao, 1985), but each one does seem to follow the same pattern: A handful of people publish an overwhelming fraction of all the papers.

We could say "We only remember a handful of scientists that advanced modern physics, so that must imply you only need that handful". Back in the early 20th century, how many physicists did "useful" work that ended up leading to currently accepted and useful knowledge? Sure we remember Einstein, Planck, Hilbert, Lorentz, Mach, Poincaré, and Minkowski. But How many physicists total were there back then? Lotka's paper samples Auerbach's Geschichtstafeln der Physik (1910) which compiles physicists the author considered sufficiently important. The book was published 5 years after Einstein's Annus Mirabilis and he's not yet cited there, Auerbach stops at the year 1900. Turns out there are more physicists than just the famous ones (Perhaps we are biased towards those that worked in one particular area that ended up changing the foundations of physics). For example we have Heinrich Kayser who did pioneering work on, and coined the expression, "adsorption". I bet you hadn't heard of him before. It wouldn't be enough to just count all the names in the Geschichtstafeln and then try to come up with a total count of physicists; even that book can be undercounting physicists that still contributed (For example, that were cited by the authors mentioned in the book). Fortunately now we have indices with journals and citations so we can truly take something closer to the entire population of scientists and explore in more detail the Ortega hypothesis.

The Ortega hypothesis

The Ortega hypothesis predicts that highly-cited papers and medium-cited (or lowly-cited) papers would equally refer to papers with a medium impact. The Newton hypothesis would be supported if the top-level research more frequently cites previously highly-cited work than that medium-level research cites highly-cited work. [From the Bornmann paper cited later]

Or to state it in a more direct way: Most science does not matter, it is a small circle of elites of today that feeds into a small circle of elites in the future.

Cole & Cole (1972) is the seminal examination of this question, which led to an entire literature around whether or not the Ortega hypothesis is true or not. They took the most cited paper from each of 84 physicists and looked at the work they cited. 60% of it was to researchers at "top nine" departments (Which comprise 21% of the entire population of physicists), 43% of citations were to researchers that themselves were highly (>60) cited [in a given period of time], despite those being only 8% of all papers. 70% of citations were to researchers that have one or more honorific awards, despite them being 26% of all physicists.

They also replicated this in a larger sample, taking the top 10 papers most cited in Physical Review, they looked at the work cited by those; so take one of those papers, get all the cited authors, compute their total citations and see if this authors are disproportionately more cited than the average author; and they are. The same is true for not so highly cited papers, leading the authors to conclude that These data offer further support for the hypothesis that even the producers of research of limited impact depend predominantly on the work produced by a relatively small elite..

It seems, rather, that a relatively small number of physicists produce work that becomes the base for future discoveries in physics. We have found that even papers of relatively minor significance have used to a disproportionate degree the work of the eminent scientists.

Nobel Prize winners, unsurprisingly are extremely well cited even before they get the award,

The average number of citations in the 1961 SCI to the work of Nobel laureates (who won the prize in physics between 1955 and 1965) was 58, as compared with an average of 5.5 citations for other scientists. Only 1.08 percent of the quarter of a million scientists who appear in the 1961 SCI received 58 or more citations. We thought it possible that winning the prize might make a scientist more visible and lead to a greater number of postprize citations than the quality of his work warranted. We therefore divided the laureates into two groups: those who won the prize five or fewer years before 1961 and those who won it after that year. The 1957-1961 laureates were cited an average of 42 times in the 1961 SCI; the future prize winners (those winning the prize between 1961 and 1965), an average of 62 times. Since the prospective laureates were more often cited than the actual laureates, we concluded that the larger number of citations reflects the high quality of work rather than the visibility gained by winning the prize.

This obviously leads to the natural white-glowing hot take one may consider: In the same way that it has been proposed to slash healthcare funding in half, for no major consequence, if highly cited science is done by a small elite and assuming citations correlate with importance, could R&D budgets be likewise be axed without any major downside (In terms of the advancement of science)?

If future research on other fieldsof science corroborates our results, we may inquire what it implies about the relationship between the number of scientists and the rate of advance in science, and whether it is possible that the number of scientists could be reduced without affecting the rate of advance. The data would seem to suggest that most research is rarely cited by the bulk of the physics community, and even more sparingly cited by the most eminent scientists who produce the most significant discoveries. Most articles published in even the leading journals receive few citations. In a study of citations to articles published in Physical Review, we found that 80 percent of all the articles published in the Review in 1963 were cited four times or less; 47 percent, once or never in the 1966 SCI. Clearly most of the published work in even such an outstanding journal makes little impact on the development of science. Thus the basic question emerges, whether the same rate of advance in physics could be maintained if the number of active research physicists were to be sharply reduced.

The authors consider some possible counterarguments to this: First, that still 15-20% of the work cited in important papers is produced by non-elite scientists and if this is relevant to the important paper then those scientists might be needed in the system as well. Their reply to this is that these scientists may be fungible; say suppose there are 3 top researchers and 100 other scientists and each of the top researchers published one paper that cites 10 papers from the rest (30 papers total) while at the same time 70 of those 100 go uncited, you could still could drop 70 of them and still get the same results in theory.

Although all scientists are replaceable in the sense that other scientists would eventually duplicate their discoveries, some scientists have many more functional equivalents than others. For example, it would be relatively difficult to replace the work of a Murray GellMann, but not so difficult to replace that of a scientist who is cited once in one of Gell-Mann's papers. If the less distinguished scientists have many functional equivalents, so do the many laboratory technicians and staff workers who often perform vital tasks in the making of scientific discoveries. We are not saying that the tasks are unnecessary, but that there are many people who could perform them.

Another critique they consider is whether the rest of the scientists perform key non-research functions, they counter this with the observation that top scientists tend to be trained by other top scientists

We know from qualitative sources and statistical studies of Nobel laureates, National Academy members, and other eminent scientists that the great majority of scientists who end up in the elite strata are trained 'by other members of the elite (22). In fact, 69 percent of current members of the Academy and 80 percent of American Nobelists received their doctora'tes from only nine universities. It might be facetiously asserted that the best way to win a Ndbel prize is to study with a past laureate. Analysis of the graduate schools attended by physicists whose work is heavily cited indicates that a large majority of scientists who turn out to be productive get their doctorates at the top 20 graduate departments.

As an aside here, Clarivate has predicted a number of Nobel award winners from how cited their work is, which lends some validity to the approach of using citations to predict actually good research. Even when the match is far from 100% with the actual choices of the Nobel committee, their picks that didn't get the Nobel still seem to count as great scientists.

Lastly, they consider the prediction question. If we can't identify who'll be good then our only hope of increasing the absolute count of top scientists is by making room for more. Here I noted that many pieces of research now seen as important were once rejected in some form or another. But previously I showed that scientists can to some extent pick among already excellent work what'll be the best. But if we're worrying about the best work, then they say that we mostly just need the top departments, and we can still have some margin of error; in physics this would involve halving the number of PhDs granted per year. They find this good for the lives and research environment of those who would remain in the system,

The data we have reported lead to the tentative conclusion that reducing the number of scientists might not slow down the rate of scientific progress. One crucial question remains to be answered: whether, if the number of new Ph.D. candidates is sharply reduced, will there be a reduction in the number of truly outstanding applicants or will the reduction in applicants come from those whom we would now consider borderline cases. This is not a matter of social selection, for we believe it possible for academic departments to distinguish applicants with high potential. It is a matter of self-selection. A reduction in the size of science might motivate some very bright future scientists to turn to other careers. The ability of an occupation to attract high-level recruits depends to a great extent on the prestige of the occupation, working conditions, and perceived opportunities in the occupation. We, of course, do not intend to suggest the advisability of any policy that would either reduce the prestige of science or the resources available to scientists. What we are suggesting is that science would probably not suffer from a reduction in the number of new recruits and an increase in the resources available to the resulting smaller number of scientists. Perhaps the most serious problem that science faces today in recruiting is the perceived reality that there are few jobs available to new Ph.D.'s. Reducing the size of science so that supply would be in better balance with demand might ultimately increase the attractiveness of science as a career.

Here, think of all the talent that is currently working at Facebook, Google, and various quant hedge funds. Suppose you could increase salaries in science to match those. Anecdotally, Pasteur was awarded, at the age of 60, an annuity worth 10x the salary of a department store worker which today in the US would be $440k for Pasteur, a salary that seems competitive with that paid by high status, high pay jobs. Rounding that to 500k, with an annual expenditure of 5bn$ one could fund a permanent college of the top 10k scientists that would be free to research as they see fit.

The authors do not recommend with high certainty that funding for science should be cut straightaway, it should be noted, in a paper I'll touch on in a moment one of them actually disavows such conclusion.

It is fitting that a pair of Coles gets a reply by a pair of MacRoberts (1986) who argue that bibliographies are incomplete. In earlier work (MacRoberts & MacRoberts, 1986) they make the critique more precise: Suppose there's a paper that builds on the knowledge of 10 other papers. Now a second papers cites the first paper but takes some assumptions for granted, and cites only the former papers instead of the former paper plus the 10 papers that underlie it. Wouldn't this lead to this one paper to be cited a lot, whereas the 10 papers that underlie it get cited less? Likewise Einstein's early work famously didn't formally cite anyone, despite it being broadly known that he was inspired by the work of others like Mach or Planck. The authors mention that this practice, informally citing without formally appearing in the bibliography is common in science. I disagree (And I've read thousands of papers over a decade across disciplines as diverse as economic history, longevity research, or psychology). It used to be the case that science was like that, but anyone familiar with modern citation practices will probably have seen that by and large this is a very small % of the actual citations of the paper. The Coles replied (1987) to the MacRoberts.

Sure there are acknowledgements that do not make it to the citation level, but this is fair, an acknowledgement implies a lesser contribution than a full citation. Furthermore, if we added these uncited papers to the bibliography, I expect the distributions would be even more skewed. Consider for example what would happen if the already highly cited PCR paper by Mullis et al. (1986) were cited every single time we see "PCR" in a paper. I expect the distribution of unacknowledged work is more skewed even than that of acknowledged work; but this is an assumption that would have to be tested. Ultimately the MacRoberts are right: if a) unacknowledged influences are highly important and b) Those influences are more widespread than the observed distribution of citations and c) Those specific scientists are relatively hard to replace (That is, that publication wouldn't have been made by someone else, who would have been more productive in the counterfactual). Then the Cole and Cole conclusion wouldn't hold: Masses of relatively unknown scientists would turn out to be key contributors to highly cited papers.

Turner & Chubin (1976) consider an alternative explanation: that the differences in raw talent are genuine, but marginal (Something I consider implausible given research on intelligence and creativity). But to the extent that this is true and that luck ends up leading to a randomly selected scientist to become more prestigious (a Matthew effect) then we could observe a similar distribution. I'll review direct evidence for the Matthew effect in the next section. The Bornmann study I mentioned previously and that I will discuss in a moment, considering a fairly large dataset does not seem to agree with the author's critique, but they [Bornmann et al.] don't offer a good reply, theirs is a replication of Cole & Cole in a larger sample, and as such is open to the same critique, we have to examine the Matthew effect directly.

I tried to look for natural experiments that claim to validate or disproof the Cole&Cole paper. One example I noted here at Nintil was that the total number of scientists as well as the % of scientists within the population and total R&D funding sharply increased during WWII. Despite the fact that there are more scientists than ever (even as % of the population) that hasn't obviously changed the growth of the US economy. In fact, most commentators, if anything, will point to its slowdown. If all scientists contribute equally, all else equal, I would expect that more R&D and more scientists almost linearly leads to more output, but this doesn't seem to be true. Unfortunately this is far from a clean experiment because TFP and GDP growth have all sort of determinants other than scientists doing science.

Another quasi experiment was the increase and later decrease in the hiring of physicists (Assistant professors) between 1963 and 1975. What does good work=f(scientists) look like? Cole & Meyer (1985) look at this:

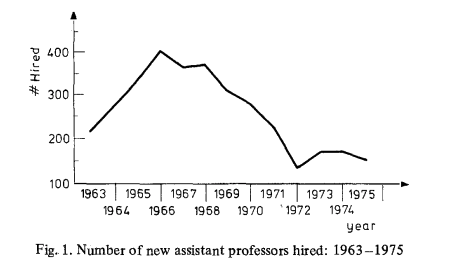
And examine the productivity of each cohort, as measured by publications in Physical Review and Physical Review Letters (The reason for picking those two journals is that they are generally agreed to be the top physics journal and they have existed since 1963; if more journals were included then citations would increase just because in the period 1963-1975 more journals were founded which would lead to more citations being possible over time)

Three hundred and seventy-six, or 45%, of new assistant professors hired between 1963 and 1965 did not receive a single citation throughout the 11-year period. Only 212, or 25%, received five or more citations to work published in one or more of the four periods. In general, those physicists who begin their careers by publishing work which is cited are far more likely than those whose early work is not cited to continue to produce high impact work.

Despite that, we don't really see a change in the proportion of physicists that ended up being cited:

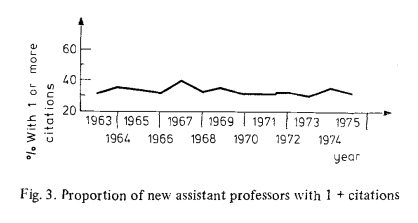
This is the author's interpretation:

The data presented in this paper offer empirical support for the implicit assumption in the work of both Merton and Ben-David that scientific advance is a function of the number of people entering science. The data does not support the assumption of Price that the number of "good" scientists grows at a slower rate than the total number of scientists nor does it support the assumptions of the 1972 Ortega hypothesis paper that we could reduce the size of science without reducing the rate of scientific advance.

(This is quite nice and honest given that the Cole of the same paper is the same Cole as in the original paper). This is not straightforward though: The paper can be taken to show that during the period studied we were not "scraping the bottom of the barrel", that we can still add physicists capable of making contributions. Or that for hiring we can't distinguish between good and best. But it still can be true that most of the ones that were added did not make a high impact contribution. If (And this is a sizable if) we can identify them ahead of time, then we could just not hire those? The paper also explores another question of why there has been a decline in the number of talented young scientists and here they point to a tighter job market for science.

More recently Bornmann et al. (2010) studied the same question:

Looking at a large dataset comprising all the papers published in 2003 by over 6k journals in various fields (i.e. 249k papers in the life sciences alone), the authors take all the papers those papers cited and examine what the distribution of citations look like,

The Ortega hypothesis predicts that highly-cited papers and medium-cited (or lowly-cited) papers would equally make references to papers with a medium impact (papers in the 50th or 75th percentile). The Newton hypothesis would be supported if the top-level research is more frequently based on previously highly-cited work (papers in the 99th percentile) than that medium-level research cites highly-cited work. If scientific advancement is a result of chance processes (the Ecclesiastes hypothesis), no systematic association between the impact of cited and citing papers is expected.

They find that this is indeed the case, which they further add supports the case for concentrating the funding in science. They repeat the analysis for various fields (which is weaker for the social sciences; and they try to explain why), here's the result for the life sciences:

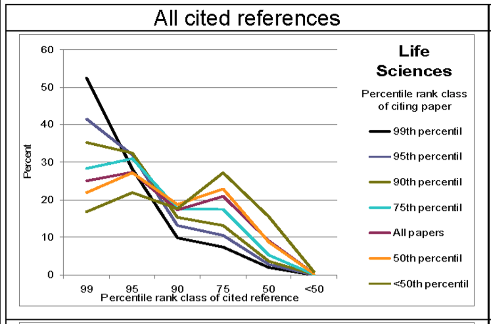
An example of how to read this: If you take all the cited papers that papers that were published in 2003 that ended up in the 99th percentile of citations (By 2010) ended up citing then over 50% of those were to top (1%) papers and less than 10% of lower 90% of the distribution were cited. If one accepts that top papers are "the best" then this is evidence that "the best" only relies on "the best" research done in the past: Giants build on top of other giants, not on top of the masses, to the extent that citations are a proxy for good work. A caveat here is that the authors did not exclude reviews; and reviews plausibly are very cited and cite the most cited work by design. But reviews are a small fraction of all published papers, so this bias is there but probably not enough to change the results. (In the top 100 of all papers ever in Web of Science, none is a review).

The Matthew effect

Highly cited scientists cite other highly cited scientists. Is this because of prestige bias, or because they are acknowledging truly good work? The affirmative answer to this is known as the Matthew effect ("the rich get richer") and was first proposed by RK Merton²

Azoulay (again!) et al. (2013) has a recent paper on this; specifically the question examined is whether becoming an HHMI Investigator (again!) affects the citation patterns of previous work, compared to a synthetic sample (If you have read my post on a different Azoulay paper you know how this goes). Of course it would be hard to disentangle the Matthew effect from genuine good work if the new work they publish is more cited: They get both the prestige of the award and the means that come with it and both could contribute to more cited work. But for past work , getting the award should not really raise the citation count by much; sure maybe some scientist missed this work and the award now gives it extra visibility. They do find a small effect that tends to wash out relative to controls over time, perhaps 10 years later. The effect is one extra citation on average. When they split the papers published by when they were published (relative to getting the HHMI award), they find that articles published 2 years and before prior to the award stay unchanged, most of the effect is driven by articles published immediately the year before getting the award; those get 3 more citations on average, and this effect diminishes over time so that 10 years after the appointment this becomes one citation; the authors attribute this to the award reducing the uncertainty of newer work by revealing that the winner has done good science as examined by a panel of experts; older work may be perceived as more solid and already cited whereas new work may be found faulty in the future. Consistent with this story, work of younger scientists is more likely to benefit from this effect, as older scientists can be more readily assessed by their peers from their longer track records. So maybe there is not much of a Matthew effect! In we average over many scientists, and look at the long term over their publication careers, the citation analysis in the previous section would continue to hold.

Li and Agha (again!), as part of the same work also try to see whether the association between higher scores given by the NIH study sections and higher citation performance later could be mediated by prestige. If the Matthew effect is there, it could manifest itself in two ways:

1. More prestigious scientists get higher scores
2. Conditional on a grant being funded and for a given score, prestigious scientists are cited more often.

A sample causal diagram is here:

The paper tries to control for prestige by using dummy variables for having a PhD, an MD, or both, and how many years a PI has been in academia. These are highly imperfect as proxies of prestige, but in any case controlling for this does not change the association between scores and citations. They also control for a set of things that sound closer to "prestige", including past funding and institution of origin, finding that this does not alter citation performance much.

Specifically, we include variables controlling for whether the PI received NIH funding in the past, including four indicators for having previously received one R01 grant, two or more R01 grants, one NIH grant other than an R01, and two or more other NIH grants. To the extent that reviewers may be responding to an applicant’s experience and skill with proposal writing, we would expect the inclusion of these variables reflecting previous NIH funding to attenuate our estimates of value-added. We find, however, that including these variables does not substantively affect our findings. Finally, in Model 6, we also control for institutional quality, gender, and ethnicity, to capture other potentially unobserved aspects of prestige, connectedness, or access to resources that may influence review scores and subsequent research productivity. Our estimates again remain stable: comparing applicants with statistically identical backgrounds, the grant with a 1-SD worse score is predicted to have 7.3% fewer future publications and 14.8% fewer future citations (both P < 0.001).

The authors can only say that prestige doesn't matter for science in general in a black box way as they don't have a model that could disentangle how quality of work and prestige play into the score, but given that overall prestige doesn't change the correlation, either a) neither of 1) and 2) is important or b) they have effects in opposite directions (Prestige reduces the odds of getting a high score and prestige increases the odds of higher citation performance, or viceversa such that they cancel out). I'm willing to accept the first interpretation, that prestige doesn't matter that much on the aggregate.

In the previous Azoulay HHMI paper they do have a model to try to predict who becomes a HHMI researcher (Table 4) but the model doesn't have that much predictive power nor can allow us to disentangle prestige from quality at the selection level.

Another way of looking at prestige and its impact is examining what happens when a scientist gets a Nobel Prize which is, presumably, the most potent status boost one can get as a scientist. Li et al. (2020) examine what happens to citations both in general (after the Nobel) as well as prior to getting it. Contrary to what one may expect, the average citations per paper laureates get goes down after the prize by around 11%, a dip that eventually recovers! In parallel with that winners author more papers in different fields (perhaps they feel like now they can explore new topics, given that they have proven themselves to the utmost extent). Li et al. do not claim these are causally related. This work also gives some indirect evidence for citations being predictive of success, given that laureates during their early careers had a more than sixfold increase over the comparison group in terms of the rate of publishing hit papers, defined as papers in the top 1% of rescaled 10 year citations in the same year and field.

There is one paper I found that shows a Matthew effect in a different context. I think this is not good evidence for the existence of such an effect in general. Bol et al. (2018) report that in the Netherlands, there is a main source of funding for young scientists, the Innovation Research Incentives Scheme. The study compares the fate of those that were above the threshold (and got the grant) and those that did not get the grant at all but were close to getting it. Those that get that grant taken as a whole get 3x the funding of those that do not, measured 8 years after the award; and they are twice as likely to earn a full professorship. This is partly (10-26% of the effect) caused by the nonwinners being less likely to even try to get more funding in the future. Note that there is the same problem I noted for the comparison group in the NIH Director's award review here, despite this paper comparing scientists that were slightly below and slightly above the cutoff threshold, the scientists in those two groups are almost a standard deviation apart in citations, number of publications, or h-index. Digging into the supplemental data, looking at citations (because ultimately impact is measured by citations and not by how much money they got), the difference between the group that almost got the grant and the one that failed to get it by a slim margin is reduced; the authors actually say there is no difference at all! The fact that the rank correlates with citations also seems to suppose the fact that peer review panels can identify top talent. So this is not incoherent with the analysis above.

Conclusion

The Newton hypothesis seems true, as far as citations are concerned: science is advanced by a small elite. This is not just "Einstein-level" breakthroughs, the small elite may not be 0.01% but 1-5% of the total number of practicing scientists. Even 10% would still cohere with the idea of scientific elitism. Citations at least on a first pass do seem to correlate with "good science" both casually (Highly cited classic papers) and by assessment of peers (Nobel prize panels; Nobel-winning papers are highly cited, and cite highly cited research). One can always make the critique that citations are not objectively measuring the worth of a piece of work. But what would? Yes, citations happen for all sorts of reasons (Including to garner favor with reviewers or other labs that might be more inclined to cite the paper if they are cited as well) but chiefly they happen because the work cited did influence the paper. There are various levels of epistemic nihilism one can go, culminating into the "We can't ever know who or what will be successful" so we should fund everyone equally, maximally equalizing funding. I don't agree with this, and will discuss scientific egalitarianism and lotteries in the next part of this series. I think this thinking can play a role in how science is organized, but not the only role.

In the first post of the series I said that the idea of funding a select few scientists and giving them extra resources (As the HHMI/Pioneer award do) depends on various assumptions: a) That we can pick the winners to some extent and b) That in fact there are winners (Or scientists that contribute disproportionately)

So far the evidence supports b) and to a lesser extent a). If discriminating between good and best were costless, any better-than-random selection process should be preferred to randomization. But when the former is costly (peer review requires peers to spend time doing the review), then it can be the case that the costs of the system outweigh the benefits. Ultimately the question of what's the ideal setup to allocate funding and select proposals will depend on this cost/benefit calculation. This calculation is most likely field dependent. The same is true for the kind of work that gets funded; biology will probably benefit from a lot of "fund projects" whereas physics will relatively benefit more from "fund people". If Smolin and Braben are right and the number of people that deserve this special treatment is small then potentially with a tiny sliver of total funding it would be possible to achieve outsized returns.

The Cole & Cole paper toys with the idea that cutting science funding (and/or concentrating it) could be beneficial. This possibility is real and worth exploring, even experimenting with on a limited scale. This of course will be highly controversial: It is easier to add funding unequally than subtract it unequally.

In the next post I will consider evidence for an alternative (on its extreme form) or complementary (in a weaker form) approach to the elitist "fund a small elite very well": using lotteries.