One of the hottest topics right now in the world of meta-science is using lotteries to fund research. In a nutshell, the rationale is that it's hard to tell who or what will be successful, and it is very costly to try to do so as well. A system that relies on peer review demands of researchers time to write grants and to review them. I have reviewed before the effectiveness of peer review at figuring out "what's good" in the context of grant awards, finding that peer review as currently practiced does substantially better than chance at predicting future impact, especially for the most impactful of the papers; but at the same time is is far from perfect, leaving plenty of variance unexplained. The way I see this is that reviewers can identify what's obviously not great and what is obviously great (Perhaps identifying the latter is easier than the former). But there is a "messy middle" where it is unclear what to fund.

Peer review systems are not cheap. In the case of Australia, Gordon and Poulin (2009) say that the cost of peer review is greater than just giving everyone a grant. It gets worse. Guthrie (2018) reports that:

The burden of the peer review system is high and falls primarily on the applicants. The overall monetised cost of the peer review system, including application preparation, has been estimated to account for as much as 20–35 per cent of the allocated budget (Gluckman, 2012). Graves et al. (2011) report that the monetised costs of the application system for NHMRC are $14,000 per grant, whilst extrapolating RCUK (Research Councils UK, 2006) estimates suggests that the costs of the application process are 10–17 per cent of the total cost of research. An evaluation of the CIHR Operating Open Grants Program (OOGP) found the application cost of OOGP grants to be Can$14,000 (Peckham et al., 2012). A detailed review of preparing grants for NIH for nursing research reports similarly high costs to institutions (Kulage et al., 2015). When providing congressional testimony individual researchers have estimated that as much as 60 per cent of their time is devoted to seeking funding (Fang & Casadevall, 2009).

This may seem excessive, but we can do a quick calculation to show that this is not farfetched. Assume that there are only PIs participating in grant application and reviews. The H's here represent time, with S being success rates (In applying for a grant or getting a paper published). 2080 is how many hours of research would there be assuming (This is far from true) a 40 hour week job. I have taken the total number of PIs from here and number of published papers from here. The time it takes to write a grant varies between 170 to 270 hours, with the average being 200 (Boyack et al., 2018). With these assumptions, or any plausible changes to them, we see that the average researcher would indeed be spending 60% of their time seeking funding. Increasing the 40 hour week to a 60 hour week (3120 hours) would still imply 40% the time spent on applying for grants. The cost of peer review is largely dominated by applying for grants, not peer reviewing. My model assumes that the average PI would be reviewing 13 papers a year. This is all averages; my model implies that on average a PI is writing 5 grants a year. Here's a case of spending 120h to write a grant, and having to apply 7 times on average. The point is that if the numbers are roughly correct, the conclusion that scientists have to spend a lot of time applying and reviewing for grants and reviewing papers is inescapable.

$$H=H_{research}+H_p+H_{other}+H_g=2080\\ H_g=\frac{H_{one\space grant}}{S_{grant}}=\frac{200}{0.2}=1000\\ H_p=\frac{N_{papers}}{N_{scientists}}*\frac{H_{{one\space review}}}{S_{{journal}}}*N_{reviews \space per \space paper}=\frac{115000}{30000}*\frac{5}{0.3}*4=256$$

This is not, to be sure, and it is important to remark so, directly related to the number of hours of researcher time that are lost to peer review; that is if there were no peer review the total hours of science being done wouldn't double despite PIs spending half their time applying for grants. This is because the research workforce has more members than just PIs. If an average lab has 7 members (including the PI, Conti & Liu, 2014; Cook et al., 2015) and they all work the same number of hours, removing the grant system altogether would not yield 2x the hours of science, but just 1.16x more. But! This would be undervaluing the benefits for at least two reasons: a) The PI role may be special; an hour of them may be worth more than an hour of the graduate student and above all b) Not being bound by the grant system means that labs might explore riskier ideas. This, I expect, would be the key channel through which the benefits of not having peer reviewed would accrue, and this would have to compensate for an an increase in funding for work that wasn't as good (And that wouldn't have made it under the peer review system).

Academic salaries and incentives

Academia is weird. In most jobs you get paid a salary that accrues for every hour worked. In academia many PIs are on soft money positions; they are only paid for part of the year and the rest they are expected to get grants for. Moreover if they don't get grants they get kicked out of the system. Even tenured professors, if they don't get grants could probably be passive-aggressively forced out. Grants are also needed to support the lab, the university pays the basic salary but running a lab, especially in the life sciences involves hiring postdocs, graduate students, and buying reagents and equipment. So academics, both to progress and stay in the system have to get grants. Perhaps getting a grant may be more important than what the grant is for, leading to a situation where PIs say they will work on X where they actually do Y which they consider more worthwhile. In theory that shouldn't matter: Funding agencies value novelty, but in practice what matters is not what you think is novel, valuable and worthwhile but what you expect the panel to judge as so.

Why is this the case? Why is science funded like this, at least in the US? Bourne (2018) says (without citation) that back in the 70s, 75% of the salaries were paid directly by the university, whereas now that number may be more like 35%, so it's not like it has always been like that. It would take a longer post to go in depth on this topic.

Scientific egalitarianism and grant efficiency

Science is highly unequal (Peifer, 2017): 10% of PIs get 40% of the funding, 20% of them get 56% of it, and 1% gets 11% . This is not necessarily a bad thing, some projects may need more funding than others. Peifer argues that there are diminishing returns to grant money, so if one wanted to produce a set of papers that in the aggregate get the most citations, funding should be made more egalitarian. One could still say that what matters more is the most cited papers, not maximizing the average per paper and in that case funding inequality could be justified. Peifer documents that more than half of the labs producing the most cited work have less than 21 points on the Grant Support Index (GSI; That is, 3 R01s or less). Anecdotally, a reason why Ed Boyden couldn't get funding for his work on expansion microscopy was that he already was holding "too many grants", so the NIH is formally or informally doing some version of this (His lab may be 6x as large as the average lab, so it's not necessarily the case that they do very expensive projects; they may be just doing lots of them in parallel).

Wahls (2018) concludes the same, that PIs should each get 400k$ to maximize return on $ spent as measured by total citation count (As it happens that's not too far from an R01). A more generous cap, of 1M$ per investigator, coupled with additional grants of 200k$ each would free up money to support 10000 additional investigators (This implies increasing the total number of funded NIH researchers by 38%).

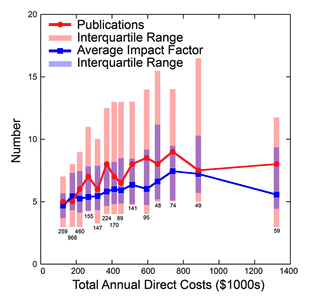
Wahls doesn't say if this would reduce the number of impactful publications. Plausibly more expensive grants are required for more impactful research? Wahls cites a couple of papers to support the "cheaper grants are more efficient view". Lorsch (2017) refers to an earlier study done on NIGMS (National Institute of General Medical Sciences) that shows that the peak in terms of impact and impact factor (of the journals where the papers end up) is substantially higher than R01; the peak seems to be somewhere in the 600-1000k$ range. In the figure, oddly there is a (unexplained, in the paper) sharp drop in productivity beyond that range.

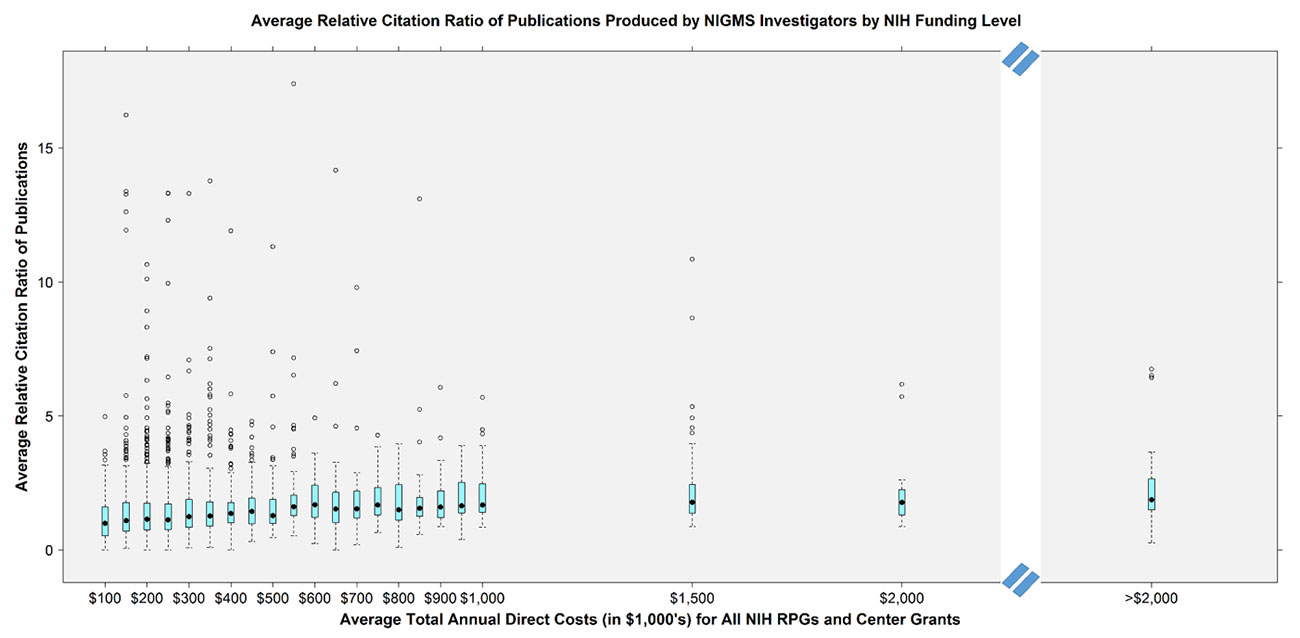
Basson et al. (2016) does look at (a normalized measure of) citations (Again, NIGMS) in the period 2011-2015 and here there does not seem to be much of a trend; in fact it seems most of the very highly cited papers are concentrated in the sub-500k$ range.

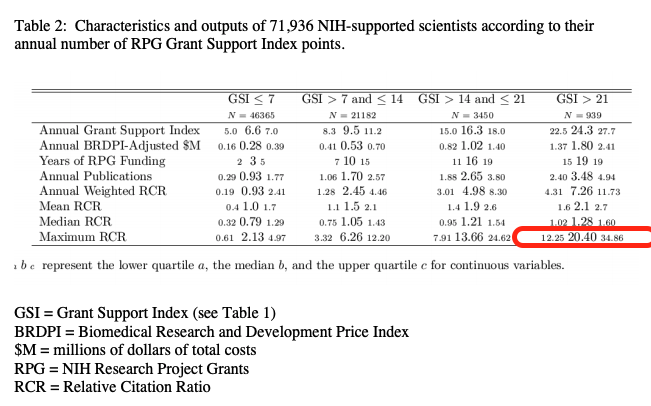
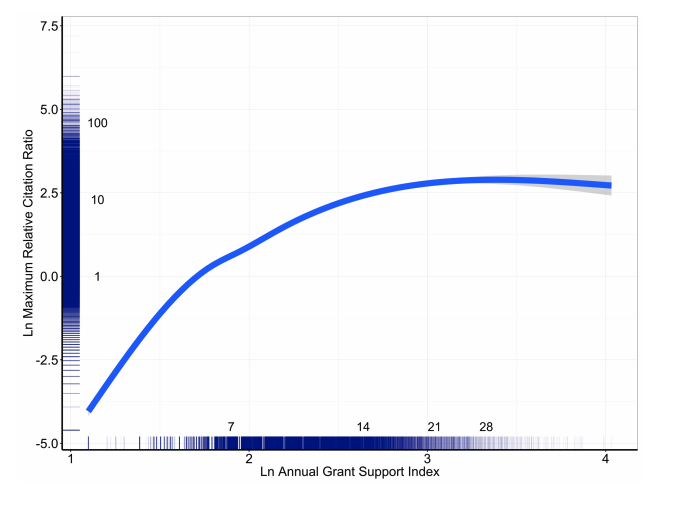
Lauer et al. (2017) includes all NIH-funded investigators in the period 1996-2014 (71k PIs) that published 1M papers. Table 1 has some summary statistics bucketed by GSI (An index of how well funded a PI is; an R01 is equivalent to GSI=7); the (mean, median,max) relative citation ratio goes up substantially with a higher GSI, below I highlight the maximum as I'm particularly interested in that as a proxy for outstanding research; the mean goes up by 2x, but the maximum goes up by 10x which is quite significant. The fact that all impact-related metrics go up adds robustness to this.

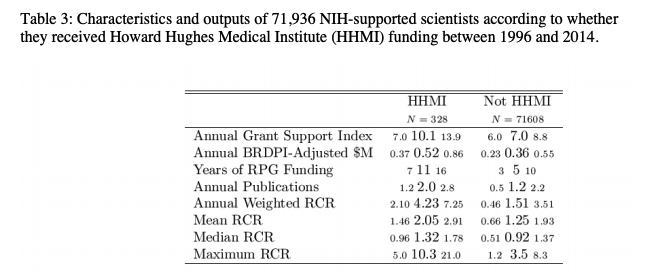
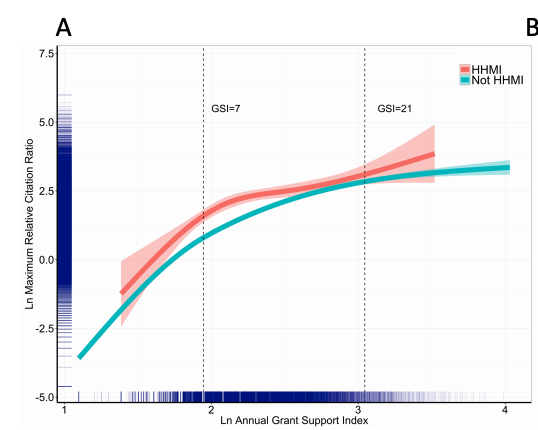
The paper also takes our favorite researchers, HHMI investigators, who are (either because of the award or due to their intrinsic capabilities) more productive than the rest and considers them separately. Unsurprisingly no matter mean, median, or maximum, their work is more impactful. In fact, if you take the average maximum RCT from the lowest quartile of HHMIs (5.0), that's higher than the median maximum RCR of non HHMIs. Looking at the median would be highly misleading here; HHMIs don't seem that much more productive, their outperformance does not come from publishing more, it comes from publishing more extremely well cited papers.

There are decreasing marginal returns to producing the most highly cited work In the general sample, as shown below. Beyond 21 there doesn't seem to be much of an increase.

The same is true by breaking the sample by HHMI status. Both axes are log-transformed so it's hard to appreciate the differences between both groups though.

The curves look similar for the mean or the median, so if one had a fixed amount of money and wanted to maximize marginal productivity per PI one would fund in the range that's around the peak, between 0.25 and 1 million. This is where the recommendation above comes from.

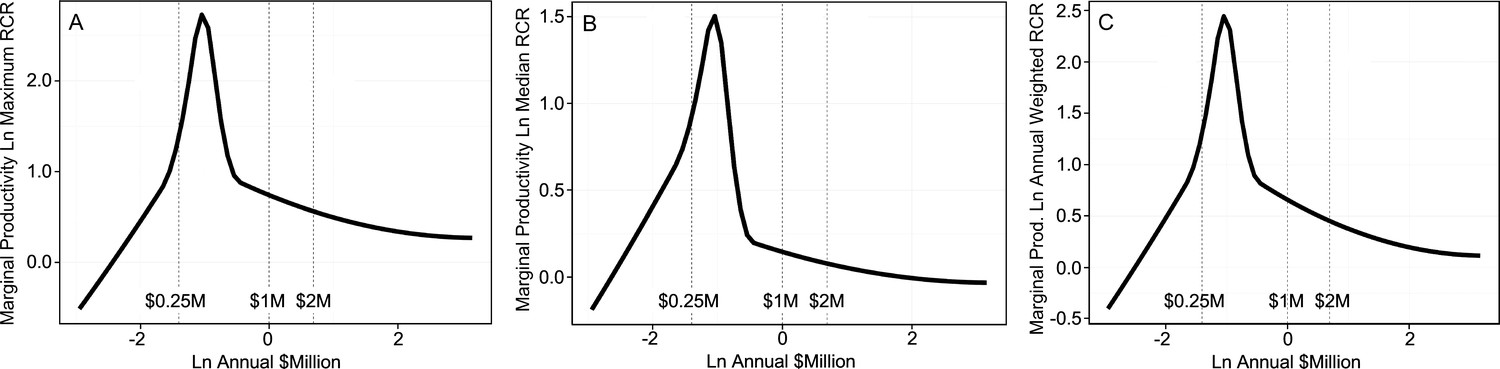
But! Note that the marginal productivity doesn't become negative, it tends towards zero. It still remains true that productivity continues to increase with more money, it's just that it goes down, so whereas we can say that if we want to get more papers period grants should be capped we can't necessarily say the same for maximizing the maximum RCR per investigator based on this. Additionally, it can be that the amounts required for any given project are project-dependent; it is one thing to want to maximize the sum total of RCR or even the number of papers in the top 1% by RCR but another one is maximizing "good science" done. Getting high RCR papers in field A may be cheaper than doing to in field B, but if both fields are reasonably important then this means that by unit of science (whatever that may mean), B projects are going to be more expensive not due to any inefficiencies but due to the intrinsic higher costs of that field.

Another point here is that accepting the decreasing marginal returns, we have to wonder if this is driven by single labs becoming more inefficient with scale, or if high RCR papers are by their nature more expensive; it is plausible that as labs get bigger they may introduce inefficiencies (The opposite is also true, it has to be tested empirically), but it also seems true that rewarding high performing labs with more grants is not a bad thing if they are higher performing due to their organizational characteristics or the specific people that work there rather than because of a Matthew effect.

Aagard et al. (2020) review the literature on whether funding should be dispersed or concentrated on elite researchers. They point to a strong inclination toward arguments in favor of increased dispersal. Let's break that down:

First, in favor of concentration they point to the following kinds of arguments:

• Efficiency: More concentrating funding may lead to economies of scale (A single lab may reuse equipment or knowledge that would otherwise be duplicated)
• Epistemic factors: Giving more resources to a small number of elite scientists should lead to better science
• Organizational conditions: By pooling resources, it's possible for labs to hedge their bets and be able to engage in riskier projects without risking the reputation of the lab in the process. (Say if you have 10 labs doing 10 projects they may choose 10 safe projects; if there is 1 doing 10 projects they may fo 5 safe projects and 5 risky ones, even if 4 of those fail they can still 'show their work' with the rest and justify the portfolio as a whole.)

Second, against concentration and in favor or dispersion ("egalitarianism"), we have:

• Efficiency: As highlighted in the articles reviewed before in this post, more funding can lead to decreasing marginal returns. Also, concentrating grant funding can make PIs into managers that spend all their time applying for grants instead of doing research or mentoring students.
• Epistemic factors: As with efficiency, spreading funding may lead to more and higher impact outputs. Funding multiple labs will increase the number of approaches that get tried, increasing the chances that one of them finds something impactful.
• Organizational issues: More labs mean more and more diverse opportunities for students
• Peer review: Concentrating funding requires deciding who should get the funding, implying a peer review system. To the extent that this system is biased, unreliable, and risk-averse, this is a negative of concentration. This is another way of expressing the idea that even if scientific skill is highly unequally distributed, if we can't measure that distribution (except perhaps ex-post), we may as well fund randomly.

So far I see all these arguments as hinging on what the distribution of talent looks like, and what ideas are a function of; if coming up with ideas is just a matter of time then the more people the better; conversely if that also depends on how good the individual scientist is then the benefits of having more heads can be offset with a higher chance of a breakthrough per individual. It also depends on what are we interested in maximizing. Is it just papers published? If we think that it is only a small part of the science that matters, and that such science can require more resources then even when on paper it is in the decreasing marginal returns part of the curve, funding that is still the right thing to do.

Most of the papers studying the correlation between funding levels and outputs (publications, patents, citations) find either constant or decreasing marginal returns, but these results seem to be heterogeneous as to where the cutoff for the onset of those decreasing returns would be. The authors also note something that to me make drawing conclusions not at all straightforward and that I mentioned earlier:

However, reducing the issue of funding size to a simple question of evidence for or against concentration would be to oversimplify a complex and multifaceted problem. The “proper” balance between concentration and dispersal of research funding may be more accurately described as a matter of degree: Both too small and too large grant sizes appear to be inefficient in both economic and epistemic terms. Notwithstanding, the available research suggest that the funding levels needed to achieve a “critical mass” may not necessarily be very high. Hence, a key question concerns where the “sweet spot” (or preferred region) in the balance between concentration and dispersal is to be found (Page, 2014). Given the presumed benefits of funding dispersal with respect to diversity, there is an urgent need for more thorough and systematic examinations of how much diversity and which forms of diversity that could accommodate a more robust, innovative, and forward-moving scientific system (Page, 2014). The optimal balances are, however, likely to be dependent on both field-specific characteristics and factors related to the overall configuration of national funding systems.

So whereas I have no problem in agreeing with the authors on something like "All else equal funding should be dispersed", the problem lies in that all else equal.

As a thought experiment, Vaesen & Katzav (2017) have the actual numbers that would result from funding everyone equally in the Us, the UK, and the Netherlands. I focus here in the US case. The calculation is based on total federal R&D funding in the US to universities from NIH, DoE, DoD, NASA, USDA or NSF (36.68 bn$), and the total number of faculty employed at universities (317k) plus 200k PhD students and 62k postdocs. Given this they estimate that each faculty member that's doing research would get 599k$ for a five year period, plus another $418k to pay for hiring and materials. This would be equivalent as giving everyone 2-4 NIH R01s.

We can redo the calculation for NIH alone; NIH spends 29bn$ per year on 55k grants; from the Lauer 2017 dataset above there may be 30k PIs funded per year (Coherent with this). So we get roughly 1M$ per PI per year? This is substantially more than the 599+418 that Vaesen & Katzav mentions above, as that is for 5 years. This may be due to them including literally everyone that is employed by a university in the US doing research of any kind (317k) and my PI calculation is including just PIs (30k) that did get funded in a given year. We could still get to 500k per year and still double the number of PIs NIH Is funding.

Going to that Lauer dataset again, assuming funding worked like this we can compute what would happen had we given everyone 1M and assuming, very naively, that projects that cost more than this would not have happened; then NIH would have still been able to fund 84-90% of PIs on any given year. Out of the remainder, on average those PIs would have needed another 1M$ in grant money to be able to complete all the grants they actually got.

But these results may be biased due to the fact that some fields or grants may be intrinsically more expensive than others. So to see what the correlation really looks like we would need to introduce something like PI-level fixed effects (Assuming that a PI works in a given field) in the models Lauer et al. are using.

Fortin & Currie (2013) to some extent overcome the field-dependent problem, as they split their analysis by field. They consider grants (up to 139 per field) given to the set of researchers funded by the main funding authority in Canada (NSERC), and consider a number of impact metrics (publications, citations, most cited article, number of highly cited articles). They find that there is almost no correlation between funding and output, and variability in outputs is so the most cited article of a highly funded researcher was 14% less cited than the most cited article from a pair of random researchers that received half the funding each. So here, clearly, the conclusion that funding should be spread thin does seem justified. Also, taking researchers that had their funding increased did not lead to more publications; rather researcher performance seems to be intrinsic to that researcher,

We postulate that scientific impact, as measured by bibliometric indices, is generally only weakly money-limited (although other important impacts of grant support such as training of students probably do scale closely with funding). Nobel Prize winning research may be highly funded, or not funded at all [18]. At present, we can only speculate about why impact varies so greatly among researchers: perhaps differences in training, in career stage, in other responsibilities (teaching and administrative), in institutional priorities, or perhaps differences in something ineffable, akin to talent. Whatever drives impact, it largely persists through time in individual researchers

This particular result is not true in the case of NIH research; if we take Lauer's dataset (Code available at the Nintil repo) and sample 2 PIs that were funded around the median and 1 PI that was funded 2x the median, we take the max RCR from both of those groups and repeat the process 50000 times, about half of the times the one highly funded PI has a higher maximum RCR. But when quantifying that difference, looking at the mean of the ratio between the RCRs of the high and low funded researchers that number is 2.56. So rather than the 14% advantage for egalitarianism that Fortin & Currie found, the Lauer dataset shows that the number is 256% for NIH funded researchers using a similar methodology. Maybe this is because this sample is larger than Fortin & Currie's (More space for outliers), or it's a quirk of the RCR as a bibliometric indicator, or maybe NIH papers just have high variance in general. Another check I did (See notebook) was to see how max RCR behaves as we draw more researchers from the distribution. Does sampling more researchers that got funding around the median increases the maximum RCR (on average)? If we were sampling from a normal distribution the answer would be no, we saw this before (Note 2 here), but here we get increasing maximum RCR, so buying more variance by spreading the funding seems to pay off.

But! If we take work in the top 1% by RCR (>59.29), we see that the median funding for those projects was almost 1M$ (More than twice the median), and so we have a situation similar to my comments on the Li & Agha paper: That high funding does not imply high impact while at the same time high impact more often than not necessitates high funding. The pattern is similar across impact categories (Upper 0.1% RCRT quantile, or 0.01% RCR quantile).

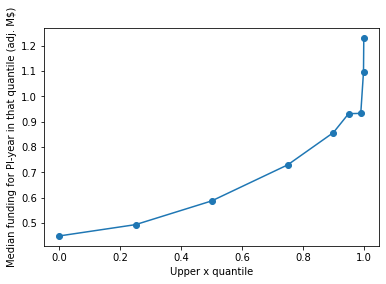
So rather than doing Fortin & Currie do, we could wonder as well how many top papers would result if we institute a policy where no PI gets funded with more than a given amount; First I sample 100k PI-years from each bucket. I find that a funding cap would decrease the number of papers in the top by RCR.

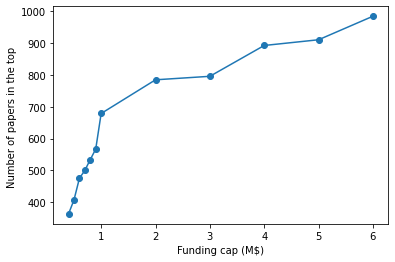
This is unfair to the cap because a cap means we can fund more grants for a given budget, so let's repeat the exercise from before (Sampling either 1 highly funded PI or N PIs with k the funding each), N=1/k but instead of seeing who got a higher RCR, seeing how many highly cited papers we get in each bucket. With k=2 (That is, we fund 50k grants at twice the median vs funding 100k at around the median), the answer is that the highly funded group produces more (22% more) papers in the top 1% by RCR.

Setting aside the particularities of the RCR as a metric and the problem of field-specificity, this illustrates that the optimal funding structure in science depends on what the metrics one wants to achieve are. If it's just average higher impact, then funding caps make sense, but if you want more top papers (Which makes sense if you assume that only the top counts) then there should not be caps. An argument against this would that even with less funding you can still get top results, that giving more money to some PIs will lead them to play with fancier tools; rather than being more creative in using equipment and tools already available to achieve the same ends, they may buy the latest kit that only marginally improves on the previous one. Again it's only a question that can be settled by experiment.

Janssens et al. (2017) note that the RCR, laudable as it may be to have a metric that normalizes citations by field and year is far from ideal:

The calculation of the annual weighted RCR of researchers’ portfolios assumes that the RCR of a scientific article is constant over time, but this is not the case: 8 the RCR decreases when an article is past its heyday. The citation rate of an article (the numerator in the RCR equation) decreases over time when its number of citations ‘stabilizes’ and the number of years keeps increasing. The expected citation rate (the denominator in the RCR equation) is a normalized 2- year citation rate of the journals in which the ‘field’ articles were published. Using a 2-year citation rate assumes that the citation rate of an article is constant over time and always as high as in the first two years, which is unrealistic for older articles. A decreasing numerator and overestimated denominator result in reduced RCRs for most older articles. When the RCRs of scientific articles decrease over time, the annual weighted RCR is not a suitable indicator for the current or recent scientific influence of mid- and late-career researchers, as their older work pulls down their portfolio RCRs. The reduction of their annual weighted RCR might, at least in part, explain the diminishing returns that were observed in the NIH data as researchers with higher GSI scores had substantially longer histories of grant funding (median of 19 years among GSI>21 as compared to 3 years among GSI≤7)

And what is worse, NIH did not seem to have considered the idea of experimenting; rather than proposing instituting a cap they should have randomized PIs to a cap or no cap conditions and then measure outputs. That seemingly was never on the table but should have.

Thinking rationally about funding allocation in science

Imagine a lab wants 1M$ for a study and two labs want 0.5M$ each for another study in a different field. The considerations above would lean towards funding two labs instead of one. But now suppose these one lab has a track record of producing very highly cited (And acclaimed by experts) work whereas the other two are not. Or suppose the labs are equally capable, but the field where lab A works in tends to do more expensive experiments. Should the weighting be done at the level of the lab or of the field?

Now consider that the first lab works at the forefront of a new subfield of oncology and has in the past produced basic research leading to insights upon which available drugs are based whereas the second is trying to better understand an ultra-rare disease. What would you fund?

For this second scenario there is a simpler rule of thumb: Fund research targeting each disease depending on how prevalent that disease is, weighted by how serious it is. So if disease A leads to 2x the QALY/DALY lost than disease B then the former should get twice the funding. A funder might choose to give 1M$ to one field and 0.5$ to another. But within one field the question of per-lab allocation would remain.

What the studies above on efficiency are probably getting at is the suspicion that if we could control for field-specific costs then some labs are more efficient than others, and I infer that if this could be done then we could use that to tailor grants; if lab A does a scRNA-seq study in mice examining the liver and that costs C then perhaps if lab B proposes to do the same study but in the pancreas for 40% more then B shouldn't get any money, giving that instead fo researchers that pass some threshold of efficiency.

Shahar Avin (Hi Shahar!) reviewed the effectiveness of peer review and lotteries in an 2015 and 2019 articles and more broadly his PhD thesis considers funding of science more broadly; he notes that the costs of having a peer review system could be in the order of 14% of total funding, and that this system is far from perfect (I reviewed the evidence behind grant peer review here). And he also discusses a potential downside (or upside) of a lottery system: Under a pure lottery scientists wouldn't be able to rely on say 10 or 20 years of continuous funding, they won't know if they will draw a ticket in the next period, and nothing they can do can change that.

A point, so far undiscussed (I was hoping to have a post that deals exclusively with bibliometrics at some later time) that he raises is that one can look at citations and RCRs as much as one wants. But what we should care about is the social value of science: Science is too important to be left to the scientists and the way science is structured is just a means to pursuit of whatever is it that society tasks science with. Given most people values, this is to produce research that is relevant for innovation that improve people's lives, and to a far lesser extent, to broaden the frontiers of knowledge for its own sake. If we can't know what research is going to be socially beneficial, it doesn't matter what analysis we do on highly cited research, we are back to randomizing funding by default. Is funding the nth -seq (There are so many of them now) more worthwhile than funding a cancer research paper? Even if say we expect the former will get more citations, it's far from clear that it will be the most likely way to contribute to the development of products that people will then benefit from.

Lottery proposals

During the Fund People, not Projects series I have mentioned here and there various experiments one could do to change the way the funding of science is done. A good set of them is Ioannidis (2011), Gross & Bergstrom (2019), Fang & Casadevall (2016):

• Fund everyone equally
• Fund a set of grants at random
• Fund a set of grants at random, asking reviewers if the grant has no major flaws
• Fund a set of grants at random, asking reviewers if the grant is meritorious

And I can add some more of my own,

• As above but use a bibliometrics-based model to "load the dice"; e.g. if you are an accomplished researcher you get more chances in the lottery.
• Have open-ended running for 1,5,10, and 20 years, then use lotteries for those
• As before, but for say the grant running for 10 years, have half of the researchers be "successful" (As proven by bibliometrics) and the other half be truly selected from a random pool subject to a minimum review.

The politics of science funding

A reason why we may see less experiments with funding modalities than we would like is politics. Barnett (2016) reports an answer from an Australian funding agency as to why they haven't tried lotteries: not that it wouldn't work but that it would make it look like we don’t know what we’re doing, the agency is worried about losing face and that seemingly gets in the way of experimentation. Beattie (2020) in a letter to to Nature complain that lotteries are just a way for an inefficient bureaucracy to try to cope with how science this work, calling for Academia [to] resist this bureaucratization of research and publishing by well-meaning but scientifically inept bureaucrats whereas Vindin (2020) rejects the idea of grants on the grounds that it won't favor merit or work that requires longer term funding.

Scientists in general have mixed opinions on the idea of lotteries. Philipps (2020) interviews 32 scientists in Germany both senior and junior and spread across the life and physical sciences, whereas they express support for the idea of peer review, they also think that lotteries should be given a chance, but perhaps not in a fully randomized way; for example one of them said that if it's truly random that may lead to researchers to write lots of lower quality grants just to have more tickets in the lottery. This highlights that lotteries could be done at the researcher level or at the project level; Lotteries work both in a "Fund people" and a "Fund projects" world.

Liu (2020) is another, broader survey in the same spirit as Philipps (2020) but in New Zealand, and with 126 scientists. Here, scientists seem more (63% of them) in favor of using randomization for exploratory grants but in general for other grants they are almost evenly split. Some of the specific arguments given by those who opposed lotteries don't seem that good; for example "I don't think a randomisation process is any less fair than an individual reviewer finding some minor reason for a great project not to be funded."; assuming that both processes are as random, lotteries still have the advantage that they are cheaper as they don't demand any (or less) reviewer time. There seems to be some agreement with a "messy middle" lottery funding model, where "obviously good" applications get funded, "obviously bad" ones get rejected and everything else gets funded at random.

Critiques of the lottery system

Most research work on lotteries is favorable. I tried looking for research that explicitly criticisms the notion of using funding lotteries.

The only one I could find, other than the two comments from Beattie and Vindin is Bedessem (2019) seems to suggest that one argument for lotteries, that we (Or scientists in a field) can't know what will be good science because success occurs very randomly, is mistaken because

it underestimates the fact that the structure of the systems of scientific practice constraints strongly (or more strongly that assumed in pro-lottery literature) the kind of project that may be considered (relatively) interesting-that is to say, useful for a (relatively) large number of scientific practices, including technical, experimental, or theoretical activities. Because of these interconnections, it seems reasonable to suppose: 1. that there are not a large number of ‘exploratory’ projects that are strongly disconnected theoretically, experimentally, and technically from existing systems of practices; and 2. that it is at least theoretically possible to obtain a more precise comparison of the value of ‘equally good’ projects if we take into account the various kinds of objectives of different kinds they pursue.

And whereas this is true, the pro-lotteries side could reply with a) Granting that most science is exploratory, at any point in time there are more promising non-exploratory projects that can be funded. There is then a question of deciding between these and b) It is indeed possible, but at what cost? Predicting success is hard!

So while he is right in the abstract, his concerns have to be weighted with the equally valid arguments the pro-lottery camp makes.

The time factor

Assuming a lottery system, one has to decide the funding period. Relative to status quo the system would make it more difficult for projects that do need more time to succeed. Braben says that Planck needed 20 years working on the foundations on thermodynamics to arrive at the idea of postulating the quantization of energy. Regardless of whether that's literally true or not, it's true that it can conceivably be the case that the quality of the research can be a function of how secure a scientist is in their position.

How much time do scientists in general need? If most science, and most useful science, can be done in 5 years then a randomized R01 lottery in the context of NIH wouldn't be subject to this objection. If only a small minority are the ones that would benefit from super-long funding then the lottery could be coupled with another lottery that could offer longer term support.

Conclusion

The evidence reviewed here supports the use of lotteries as part of a science funding ecosystem. Proponents of lotteries may have underplayed the extent to which peer review can detect impactful work, and the extent to which citations can be tied to downstream practical applications but overall their cost-benefit analysis is reasonable. I believe a system could be designed that appeals to funders and scientists such that I get buy in, but this won't be a pure lottery. Whereas obviously I have to end this post with a call for experiments testing various kinds of lotteries, if I were in charge of implementing any such system, the way I would do it would be as follows:

• Part A "The HHMI-lite" (85% of the funding)
  • Proposals are HHMI style, relatively short, proposing a broad research idea rather than an R01 style narrow project. They are to be sorted (perhaps by a review section) just into three buckets: Must fund, May fund, and don't fund. Must fund papers are all funded. If the funding needs exceed funding available, they are chosen at random. Reviewers are limited to a small number of "Must fund" designation for the papers they review. May fund papers are all funded at random.
  • Projects requiring funding above some threshold need longer proposals and receive additional scrutiny
  • Funding is for 5 years
• Part B "The Planck club" (5% of the funding)
  • Proposals are as in Part A, but instead reviewers are instructed to select only the best of the best applicants. Within that pool of people, a random set (As funding allows) is chosen.
  • Funding is for 20 years, with a 10 year review (Only in case of substantial underperformance would the other 10 years not be awarded), and additional money is available for equipment.
  • The need for longer term funding has to be justified in the proposal
  • Can only be granted once to a given person
• Part C "The PseudoARPA" (10% of the funding)
  • Here a panel of permanent program managers designs research programs and then aim to execute on them, funding scientists across multiple labs, or bringing in industry expertise, etc.
  • PMs have discretion to increase, decrease, or completely cut a given project
  • PMs are instructed to fund opportunities that single labs won't do either due to the coordination or funding requirements needed by the project they have in mind

Additionally, prohibit the use of grant money as salary, and impose on universities as a requirement that they pay full salary to the recipient of the grant. The lottery used in this proposal wouldn't be truly random; inverse weight would be given to how much money is asked for.