In a previous post I reviewed the evidence behind the effectiveness of two awards targeted at promising researchers, funding them more and for longer. The conclusion was that the evidence is not very strong and that the extent to which "Fund people" makes sense depends on other factors that we should also investigate.

Both the HHMI Investigator and NIH Director's Pioneer Award are targeted at scientists that are expected to perform well. The each require applicants to have shown success already. Ultimately, those that get those awards do produce more highly cited work. But is that because HHMI/NIH picked those that were going to win anyway, or because of the award itself? Or a combination, of course.

It would be convenient if "past success doesn't guarantee future returns" in science; that while some scientists may seem successful, it's just because they are lucky. If all scientists are equally talented (An assumption that I'll call scientific egalitarianism) then "Fund winners" works and should be scaled to the entire system: We should expect rolling out HHMI-style funding to anyone leading to substantial improvements to the rate at which science occurs. On the contrary, if scientific talent is unequally distributed, perhaps highly so ("scientific elitism"), then dishing out additional time and money will lead to relatively smaller increases in scientific productivity.

It could also be that despite some scientists being intrinsically more likely to produce better work, that is so hard to see that it's not even worth trying. So this post will explore the extent to which pre-grant peer review helps to improve the quality of the work being funded.

Predicting success in science

First, we can look at whether it is possible to predict success in science in general. Given the career of a scientist so far, how much can we tell about their future?

Azoulay's own paper has a model in it that can predict who will end up becoming a HHMI investigator. Based on a sample of 466, Table 5 shows that their best model predicts 16% of the variance where the coefficients that are statistically significantly different from 0 are a measure of how many top 1% publications they have published, and being female; in fact being female seems 4x more predictive of HHMI selection than publishing a lot. This doesn't seem right, here are some potential explanations:

1. Women are after all better researchers than men (all else equal) even after accounting for publications and HHMI reviewers know this, or
2. Perhaps the rest of the funding ecosystem is biased against women, leaving more highly talented women available for HHMI to fund them relative to men, or
3. HHMI has biased their selection process to favor women

The case for peer review

I want to start here with Li & Agha (2015) as it's a relatively recent paper with by far the largest sample, and one that finds a result that runs counter to the anti-peer review narrative that seems prevalent in some corners of academia: they find that getting a lower (better) score by a study section at NIH leads to more citations, patents, and publications coming out of that grant in a dataset covering all R01s given by NIH in the period 1980-2008, 56% of which are new applications and the rest are grant renewals.

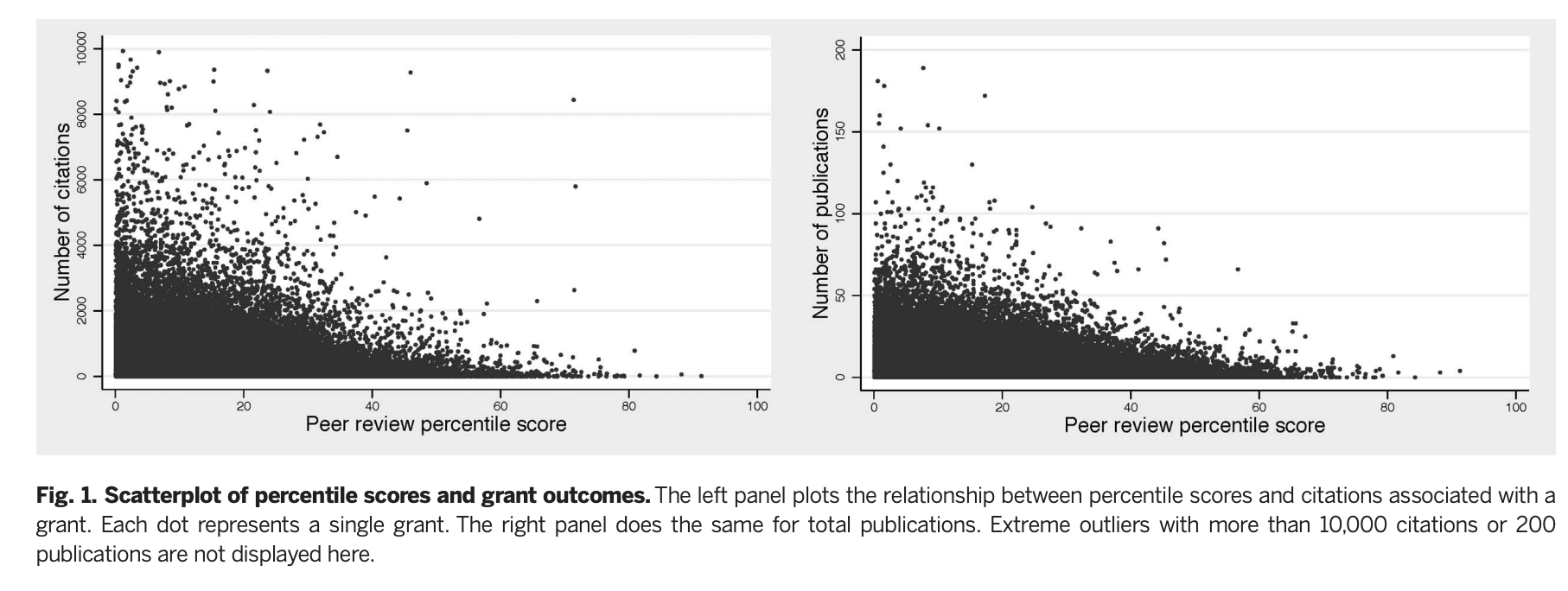
Li & Agha note:

The median grant in our sample received 116 citations to publications acknowledging the grant; the mean is more than twice as high, 291, with an SD of 574. This variation in citations underscores the potential gains from being able to accurately screen grant applications on the basis of their research potential. [...]

For a 1-SD (10.17 point) worse score, we expect an 8.8% decrease in publications and a 19.6% decrease in citations (both P < 0.001). This suggests that scores for grants evaluated by the same study section in the same year and assigned to the same NIH institute are better than randomly allocated.

Is this because the reviewers know who the applicant is, or are they using the applicant's past history to decide what to fund? There is some of this going on, and it makes some rational sense; however, the strong correlation between score and outcome doesn't go away even by controlling from other observables:

Controlling for publication history attenuates but does not eliminate the relationship: a 1-SD (10.17 point) worse score is associated with a 7.4% decrease in future publications and a 15.2% decrease in future citations (both P < 0.001).

They don't find that being for longer in the system moderates this relation, to the extent that more established PIs produce more successful work, in their dataset, it is because they do produce better grants.

Next they look at the relative impact of peer review on picking winners vs weeding out losers (Or grants that won't lead to a lot of citations)

But in their analysis the authors are looking at those that are in the top 20th percentile. In that restricted sample, do scores predict success?

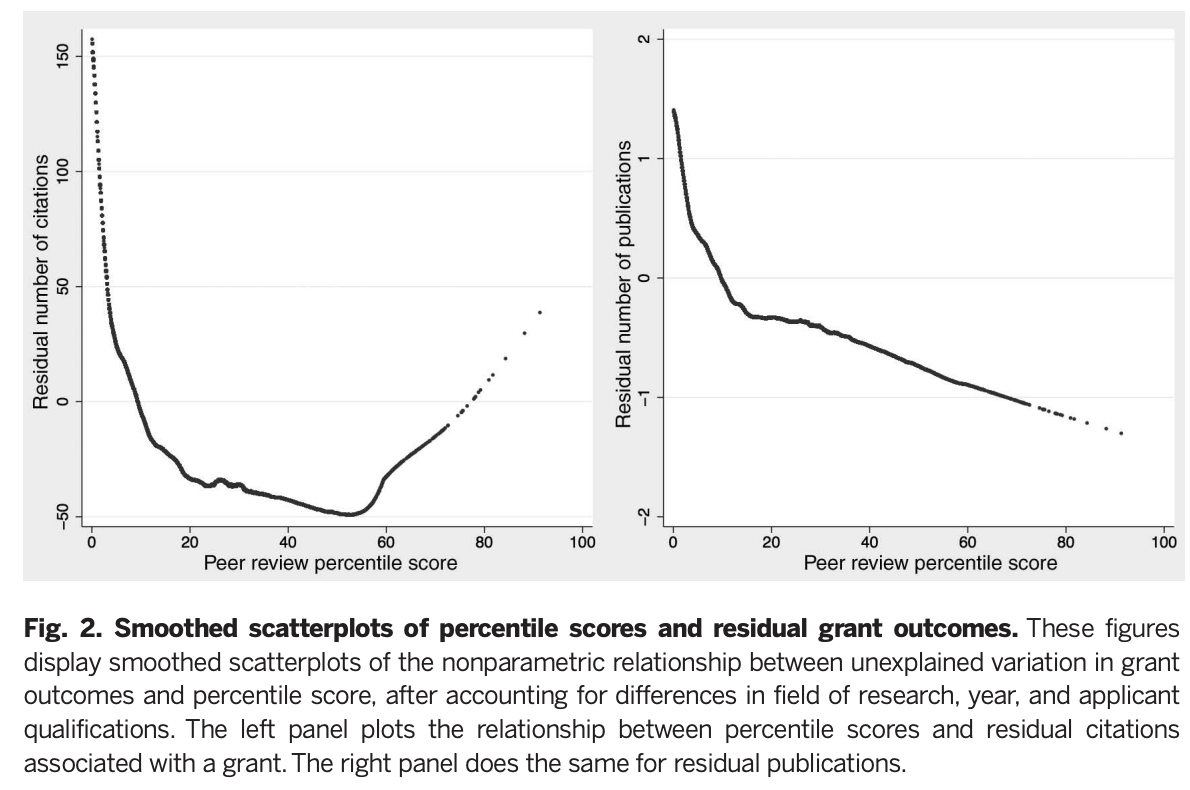
What this figure shows is the result of trying to substract everything that shouldn't matter (institution, past record, gender, time in the field) with the intention of leaving what should (Namely, grant quality). If you don't need grant quality to explain citations, then the curves above would be flat. But they are not; rather they do show that lower (better) percentile scores are associated with exponentially more citations, and somewhat with publications, especially when applications under the 20th percentile are considered. On the right tail are grants that seemed bad to the review section, but that were funded anyway. Here someone applied additional judgement to rescue a few promising papers, overruling the study section. This worked: Those papers do get more citations.

Lastly, they look at whether this predictive power is similar across all classes of publications (top 0.1%, 1%, 5% etc) in addition to leading to more patents. They find that study sections are actually quite good at discerning this great work:

As reported in Table 2, peer-review scores have value-added identifying hit publications and research with commercial potential. A 1-SD (10.17 points) worse score is associated with a 22.1%, 19.1%, and 16.0% reduction in the number of top 0.1%, 1%, and 5% publications, respectively. These estimates are larger in magnitude than our estimates of value-added for overall citations, especially as we consider the very best publications. The large value-added for predicting tail outcomes suggests that peer reviewers are more likely to reward projects with the potential for a very high-impact publication and have considerable ability to discriminate among strong applications. A 1-SD worse percentile score predicts a 14% decrease in both direct and indirect patenting. Because of the heterogeneous and potentially long lags between grants and patents, many grants in our sample may one day prove to be commercially relevant even if they currently have no linked patents. This time-series truncation makes it more difficult to identify value-added with respect to commercialization of research and means that our estimates are likely downward biased. [...]

This finding runs counter to the hypothesis that, in light of shrinking budgets and lower application success rates, peer reviewers fail to reward those risky projects that are most likely to be highly influential in their field (1, 2). [...]

Our analysis focuses on the relationship between scores and outcomes among funded grants; for that reason, we cannot directly assess whether the NIH systematically rejects highpotential applications. Our results, however, suggest that this is unlikely to be the case, because we observe a positive relationship between better scores and higher-impact

And that once one gets to the bottom of the distribution, success can be predicted algorithmically:

We don’t find evidence that the peer-review system adds value beyond previous publications and qualifications in terms of screening out low citation papers. Better percentile scores are associated with slightly more publications in the bottom 50% of the citation distribution.

This is a fortunate conclusion, because it means that it's possible to use bibliometrics to select a candidate set of sufficiently good scientists, and then use human reviewers to select among them.

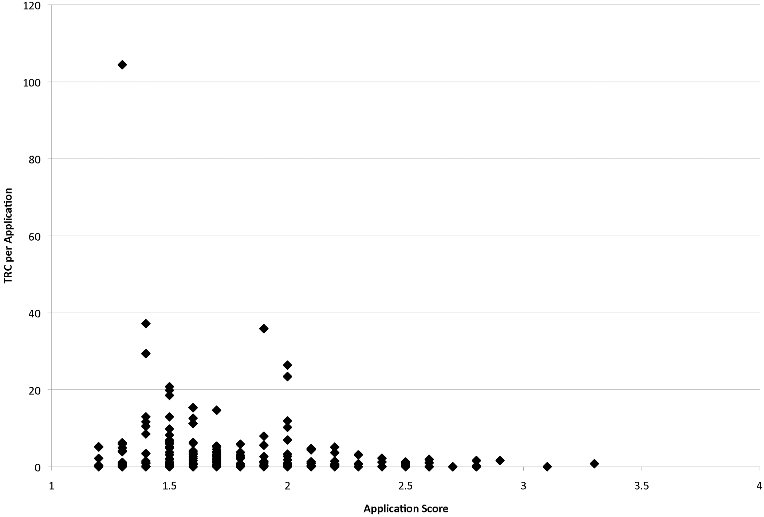
Gallo et al. (2014), using a dataset of 2063 grant applications¹ submitted to the American Institute of Biological Sciences (AIBS) find a pattern that seems coherent with the Li & Agha study, where lower (better) scores lead to more normalized citations. In particular, you can see here that there was no highly cited work (>20 TCR) with a score under 2, and the grant that led to the most citations had a high score (One that the authors removed from later analysis, treating it as an outlier! They shouldn't! Impactful science is all about these!). Now you can imagine here if you didn't have that point up there you might conclude that peer review doesn't matter that much (Perhaps under a score of 2), so having large samples that are assessed sufficiently after the grant was awarded (to allow for great work to be discovered and cited) is key. What they did find (not shown here) is that funding or seniority of the researcher alone does correlate with impact.

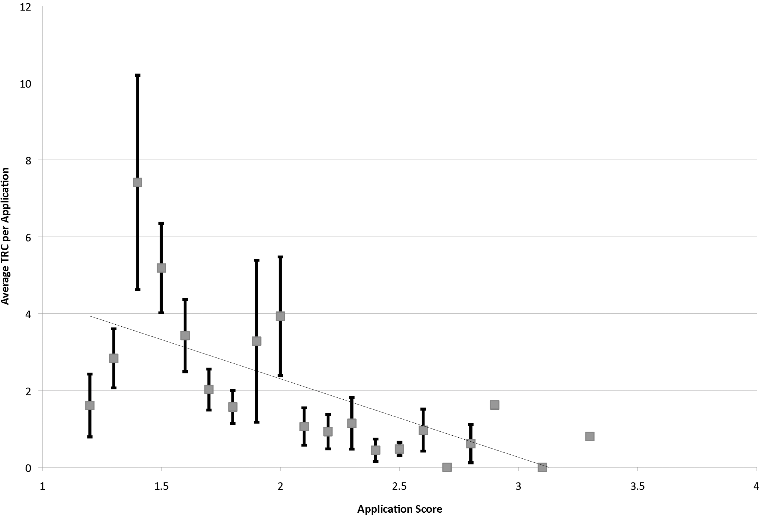
One reason the authors think their results are not quite those of other papers that find no effects is that NIH's study sections are more general than the more ad-hoc highly specialized panels AIBS uses, another is that AIBS is more permissive than NIH in funding applications with low scores (Though this is not that likely, their funding rates were even more strict than NIH's at 8% by 2006). As one may expect, when more grants were funded, the work they led to had more citations. Was this because the reviewers had a larger pool to pick from? Or just because there were more grants, period? The authors suspect it's the former, and they do have a figure showing that the average annual score was higher the more submitted applications there were² .

Park et al. (2015) are able to leverage a natural experiment to see if NIH scores tell anything about quality. ARRA was a pot of money that went to various places during the 2009 recession. This enabled NIH to fund research that otherwise would not have been funded, they found that those extra grants were not as productive as the ones NIH was already awarding, so there are indeed decreasing marginal returns, and NIH can choose what's better to some extent. Opponents of pre-award peer review can't quite say that these projects are obviously so low quality that reviewers can distinguish them: Paylines for individual NIH institutes are already very strict, so the additional grants that are getting funded under ARRA are not grants scoring 60 or 70, but perhaps 20-30.

We find that regular projects on average produce per-dollar publications of significantly higher impacts (12.5%)thanARRA projects and that this difference is primarily driven by R01 grants, the largest funding category among NIH grants. We find a similar result for the (dollar-adjusted) number of publications, and the gap is even larger: regular projects produce 17.9% more per-dollar publications than ARRA projects, and R01 grants seem mainly responsible for that difference. Overall, regular projects appear to be of considerably higher quality than ARRA projects.

Weiner et al. (2015) pool together papers chosen as "best" from a dozen of CS conferences spanning topics from ML to Security in the period 1996-2012 and ask whether these "best" papers are cited more than a random paper from the same conference. That probability is quite high, from 0.72 to 0.87. However, a potential explanation the authors do not consider seriously (They say that the best papers are hard to find in the conferences websites, but surely people in the field, especially if they were in those conferences, know what those papers are) here is that maybe "blessing" a paper with the "best" title in and of itself causes the extra citations. Unlike with NIH grant peer reviews that are not public, everyone knows what the supposedly good papers are so they are more likely to be read and cited.

The case against peer review

Fang et al. (2016) take issue with the above analysis. First, they stress that other work has found that there is no correlation between percentile score and publication productivity. Why did Li and Agha find what they find? Fang et al. say it's because they included a lots of grants with scores over 40 that would not be funded today (I don't find this plausible, eyeballing the charts provided shows the relation still holds, plus the various figures use local regressions that would be unaffected by throwing away everything worse than the 40th percentile); they also claim that *this study did not examine the important question of whether percentile scores can accurately stratify meritorious applications to identify those most likely to be productive.*yet it seems that they did so: Higher scores go hand in hand with higher productivity in Li and Agha's work. They have this figure in the paper where they show that above the 20th percentile there doesn't seem to be a lot of difference in the citations accruing to papers in each bucket, with the exception of those at the very top.

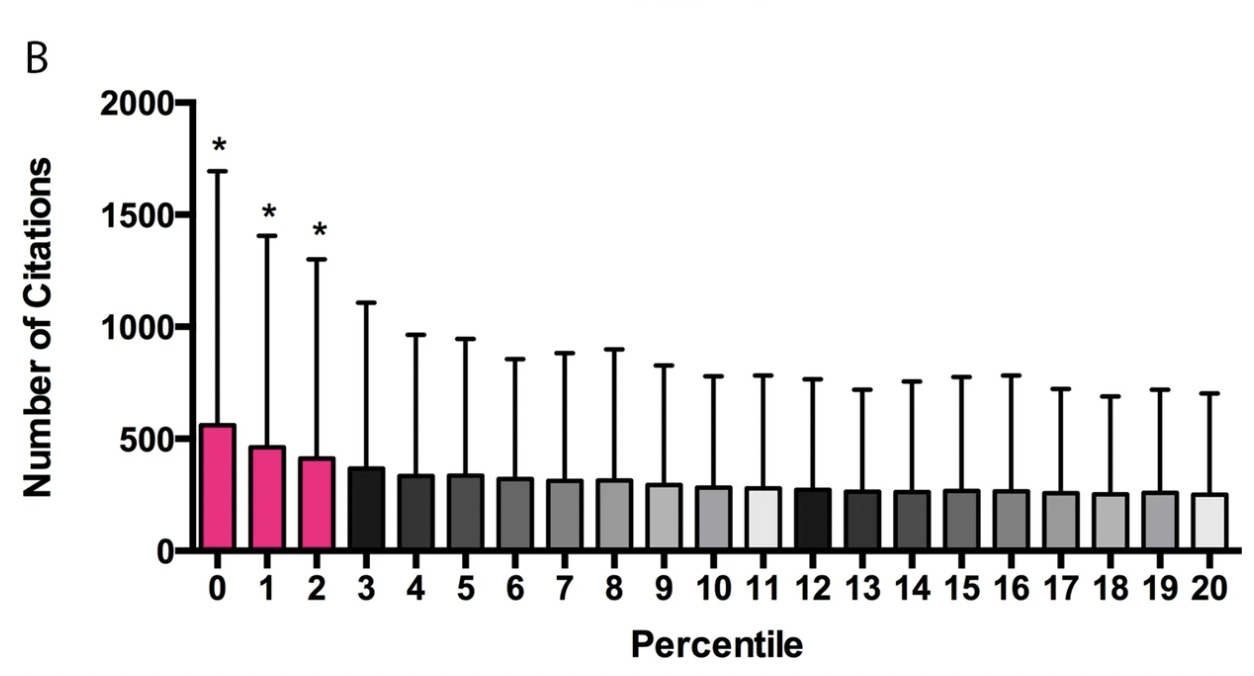
And they also point out that if one wanted to know if a publication ends up in the top 50 or bottom 50 of the distribution of publications by citation count, the predictive power of the reviewer scores is quite weak:

Li & Agha might reply to this by saying that while this is true, it may also be true that the proportion of highly cited papers is greater in the lower buckets: A good score does not imply quality, but quality tends to imply a good score. The implication is that grants were to be funded at random, fewer of the grants in the bottom (better) percentiles would get funded, and so the total number of highly cited work would decrease.

Scheiner & Bouchie (2013) examine whether NSF reviewer scores predict more cited work (Or more mean citation per year, or more publications per grant, or maximum citations among the publications resulting from a grant) among 41 projects

Reviewer scores and panel rankings were moderately, but non-significantly, correlated with project outcomes (r = 0.12–0.29), but less so when analyzed by multiple regression. [...] The weak effects of reviewer and panel assessments were even smaller when analyzed by multiple regression, due to positive correlations between the assessments and award size. [...] Peer review is able to separate those projects likely to produce publishable results from those that have substantial or fatal flaws due to conceptual defects or design flaws (Bornmann et al. 2008). And from among those proposals with publishable results, panelists can separate projects that represent exciting science from more pedestrian endeavors

I couldn't access the tables they mention for further review.

Lauer et al. (2015) is to some extent an attempt to explain the discordant results between Li & Agha and everyone else but whereas they say that Li & Agha didn't focus on normalized counts, Li & Agha explicitly tried to correct for that:

The inclusion of these fixed effects means that our estimates are based only on comparisons of scores and outcomes for grants evaluated in both the same fiscal year (to account for cohort effects) and in the same study section (to account for field effects). We also include NIH institute-level fixed effects to control for differences in citation and publication rates by fields, as defined by a grant’s area of medical application. Controlling for cohort and field effects does not attenuate our main finding.

A more interesting comment here is that Li & Agha focus on citations, but Lauer et al. say that citations per $ should be given some weight as well, ultimately seeming to settle for a middle point where a lot of research could be funded by lottery while keeping a small pot for "obviously good" material;

Thus, it seems that some of the apparent contradiction between the recent analysis of Li and Agha1 and the prior ones2–4,6 is that each focused on different questions. To maximize return on investment, it may be more appropriate for NIH to focus on bibliometric outcomes per $million spent rather than on bibliometric outcomes alone. We must acknowledge, although, that this metric has its limitations; that is, a metric like number of highly cited articles per $million may not be able to fully discriminate which projects yielded greatest scientific impact. In some cases it may make sense to spend more even for a small number of highly cited articles; for example, NIH may wisely choose to spend proportionally more money to fund clinical trials that directly affect practice and improve public health. [...]

What can we say from all this? It seems that peer review is able, to a modest extent and with modest degrees of discrimination, to predict which grants will yield more top-10% articles.1 The modest degree of discrimination reflects previous reports suggesting that most grants funded by a government sponsor are to some extent chosen at random

Danthi et al. (2016) is in some sense a similar approach to the Park study: Looking at the differences between regular R01s and R01s that got funded thanks to ARRA. Danthi et al. look at NHLBI grants where as Park looked at all of them. Danthi et al. seem to conclude that funding more grants is as effective at producing citations per $ relative to the R01s, implying that there is plenty of quality left on the table. But the also say that The payline R01 grants yielded more papers, and had higher normalized citation impacts[than the ARRA ones]. The authors say the Park study is consistent with theirs, as Park says that a dollar increase in public research funding from the current scale would produce an equivalent level of scientific knowledge as a current dollar does. And they say park finds that these two mechanisms yielded similar measures of productivity. But this is not true, scroll up and see the quote from the Park paper again, they are clearly concluding that there are diminishing returns and that the regular NIH grants were more productive, both by raw count of citations as well as per $! Further, nowhere in the paper Park et al. say that "a dollar increase in public research... as a current dollar does". Maybe in the pre-print? Not there either! Maybe in a very early draft the conclusion was as Danthi et al. say but not in Park et al.'s final paper.

In 2017, Guthrie et al. did a systematic review of grant peer review to see what is it that we know about grant peer review in the health sciences. They do not cite the Li & Agha article or the Park articles which seem the most robust pieces of evidence in favor of peer review. I copy below in full what they have to say of performance prediction:

Peer review is at best only a weak predictor of future performance. Work by Fang & Casadevall suggests peer review can ‘winnow’ out bad research proposals ( Fang & Casadevall, 2012). However, recent studies from several NIH Institutes and the Netherlands have challenged the idea that peer review can effectively select the best research. Studies comparing percentile application rankings with the research’s subsequent bibliometric performance found no association ( Danthi et al., 2014; Danthi et al., 2015; Doyle et al., 2015; Fang et al., 2016; Kaltman et al., 2014; van den Besselaar & Sandström, 2015). Two further such studies found that grant review outcomes only weakly predict bibliometric performance ( Lauer et al., 2015; Reinhart, 2009). Bibliometric analyses are by no means perfect measures of performance – only capturing a proxy of academic performance ( Belter, 2015). Nonetheless, the findings suggest that peer review assessment is, at best, a crude predictor of performance.

Using an alternative metric, Galbraith et al. showed that peer reviewers’ opinions were only weakly predictive of the commercial success of early stage technologies in small businesses ( Galbraith et al., 2010).

Fang & Casadevall (2012) comment that, while reviewers can usually identify the top 20–30 per cent of grant applications, going further to identify the top 10 per cent is ‘impossible without a crystal ball or time machine’ (p.898).

The same team published a report for RAND in 2018, and that still fails to cite Li & Agha and Park. And, taking one of the studies I haven't looked at yet (Reinhart 2009), and while they do show weak predictive performance, it's on a fairly small sample. They cite the Gallo study above but not in the "does peer review predict performance" section. This is a recurring theme here, it seems everyone is finding weak or nonexistent effects in fairly small samples and strong effects when one looks at very large samples.

Another point that some of the articles make is that we should not look just at citations but their cost, and moreover the cost of running the entire system.

Another recent review, by Gallo and Glisson (2018) is probably the most recent one, covering more than just the predictive value of scores, and does cite the Li & Agha and Gallo papers (but not the Park paper) as well as the Fang and Danthi papers so this seems prima facie more balanced in what they cover. Here I'll highlight some interesting findings from this review:

• In studies that have examined the effect of getting vs not getting a grant, studies find that getting it increases productivity (citations) in general; when it does not it tends to be because applicants in general are ex-ante very productive, which indicates that if a candidate is "obviously good" they can probably get funding elsewhere. Grants that uncover "hidden gems" would then be more effective (Remember, the Pioneer Award from NIH aims to find research that is not just good but that it's unlikely to get funded otherwise)
• It remains hard to disentangle the effect of researcher productivity from the Matthew effect ("The rich get richer"/"The best funded get even more funding") and the effect of receiving a particular grant
• One of the stronger predictors of future citation performance is past citation performance, which may be due to either researchers that are intrinsically more productive, or the Matthew effect.
• They say that "[this suggests the] coarse discrimination of peer review in separating good projects from poor ones, but not good from great." I think this is fair, but I also think my comments above re Li & Agha still apply: High score does not imply high performance, but high performance tends to imply high score.
• High citations do not always imply quality "as citation values many times are higher for “exaggerated or invalid results” and that papers are often selected for citation based on their “rhetorical utility” and not “primarily based on their relevance or validity.”
• "patent productivity has some promise for use in tests of review validity, however future studies will likely require more subtle, nuanced approaches." Also, not many studies have looked at this, compared to what is available for citations. The study with the largest sample for the NIH case is the Li & Agha paper.
• " no standard method has been created that “can measure the benefit of research to society reliably and with validity”
• "Twenty-nine percent (14) are conducted without an unfunded control, and all but one of this group examines review scores and output of funded projects. Of this subset, 71% (10) provided evidence for some level of predictive validity of review decisions. Of the 29% (4) that did not, two studies used citation level per dollar spent (Danthi et al., 2014; Doyle et al., 2015) which can mask correlations, one only looked at a limited range of peer review scores, ignoring poorer scoring projects (Fang et al., 2016) and one study had a very small sample size of 40 (Scheiner and Bouchie, 2013). 71% (34) of studies listed have unfunded controls and of those, 91% (31) showed some level of predictive validity of review decisions."

I really liked that paper and if you want to read one of the original sources cited here, this should be it.

Does disagreement predict success?

So called high-risk, high-reward research is said to be risky because it may not be obvious from the outset (even to the researcher) if the project is going to get somewhere. Hence if a funder is funding this kind of research one should expect to see some amount of failure. Another potential sign that some research belongs to this class is that the reviewers themselves can't agree if it's good or not.

There is some precedent for this kind of thinking around risky bets. Under some conditions, unanimous agreement can indicate that the group may be actually wrong. Some (but by no means all) VC funds (anecdotally) let a deal go through as long as a partner says yes to it even if the rest disagree.

As it happens, there is some research on this question, at least as far as citations are concerned. Barnett et al. (2018) study over 200 successful grant applications to the American Institute of Biological Sciences. Each was evaluated by a number of 2 to 18 reviewers who awarded scores from 1.0 (best) to 5.0 (worst), the final score is the average of reviewers' scores. The outcome measured was (time-standardized) citations to the publications resulting from said grants. The measure of "disagreement" was either the range between the lowest and highest score, or the standard deviation of the score. Ultimately the answer is that no, more disagreement does not predict success, if anything the opposite is true:

Do reviewers agree on what's good in the first place?

Another way to examine how good reviewers are is to see what happens if you give a paper to different reviewers. If the scientific merit of a paper is obvious then reviewers should all agree right? Well... not always. This is more indirect evidence than trying to predict success from scores, because it can still be that reviewers are a noisy measure of the underlying goodness of a paper, and by averaging their disparate scores a better assessment is reached. But nonetheless it's a good thing to examine to get some feeling for what reviewing looks like in the wild.

Back in 2014, the organizers of Neural Information Processing Systems (then commonly abbreviated as NIPS, one of the leading ML conferences) ran an experiment to see how well its peer review system works. NIPS has a double blind peer review process with ~3 reviewers assigned to each paper, and in 2014 they randomly assigned 10% of the papers to the peer review process again, so a total of 166 submissions were peer reviewed twice. The result was that ~57% of the papers that were accepted by one set of reviewers was rejected by another. Trying to model the result, Eric Price in that blogpost fits three possible models to the results:

• Half of the papers are obviously bad and are rejected, everything else is accepted at random
• A small proportion of the papers are obviously good and are accepted, everything else is rejected at random
• A small proportion of papers is obviously good, another bigger chunk is obviously bad, and most papers are in between and chosen at random (The "messy middle" model)

In NIPS 2016 there was an assessment of the review process that while not experimental in nature, did test Price's messy middle model on the 2015 and 2016 NIPS review processes. This messy middle was 30-45% of all the papers; for example in 2015 15% were rated as "obviously good" and 40% as "obviously bad". If this model holds it still makes sense to have peer review, but it may be better to nudge reviewers towards the "obviously a masterpiece" and "why did they even submit this lol" buckets, accepting and rejecting the former and the latter, respectively. Everything else could be accepted at random.

Pier et al. (2018) ask whether NIH's peer reviewers can discriminate the good from the excellent within a pool of high-quality applications. Here they didn't look at NIH data, but replicated the NIH process, they recruited 43 oncology researchers and created 4 private study sections, with 8-12 reviewers each. They got 25 oncology grant R01 applications, 16 of which were funded in their first round, the rest after resubmissions. They had each application reviewed by 2-4 reviewers and measured their agreement by three different measures. Not only these reviewers didn't agree on the score, but they didn't agree on the reasons for the score (strengths and weaknesses they found in the paper). Here's one example (from the supplement) of how much variability there can be, with scores ranging from 2 to 7 (Where best is 1 and 9 is best)

Reviewer 1: [Score = 7] “PI has experience in DNA technology but PI needs to learn in vivo animal study and design. Proposed radiation dose is inadequate and sample size justification is not described. Significance of the study in respect 36 currently available technology/treatment is not well described. Different luciferase imaging is not innovative.”

Reviewer 2: [Score =2] “A highly focused application describing a streamlined approach for screening compounds that target glioma stem cells in preclinical models of glioblastoma… Well supported by preliminary data. “

Reviewer 3: [Score = 3] “Strengths of the application are the PI, the solid preliminary data to support the hypothesis, the research team, and the research environment. There are some concerns regarding the approach that weaken the enthusiasm for this study, but overall, the enthusiasm is high and success is likely.”

Reviewer 4: [Score = 4] “Though this application has potential to identify druggable target/s, this proposal suffers from several flaws including 1. Open ended; 2. Interdependent aims; 3. lack of definite target/s. These problems reduce the enthusiasm for this otherwise promising proposal.

Here's a case where reviewers gave an application similar scores, but pointed to different weaknesses

Reviewer 1: [Score = 4] “Lack of preliminary data… dampens the enthusiasm of the proposal… Most of the proposed work is already established in other cancel models; hence the innovation of the study appears to be moderate. The experimental design needs more information on the power calculation of the number of patient samples and also for in vivo work. Overall, it is an very interesting proposal with a well-qualified team; however, lack of details diminishes the significance and the impact of the proposal.”

Reviewer 2: [Score = 3] “This is an excellent proposal… Dr. Rice is an expert in IGF-1R signaling and its role in breast cancer progression. She has enlisted the help of strong collaborators with expertise… Together this is an outstanding investigative team… The proposal is conceptually innovative, although it is not technologically innovative. The aims are logical and the experiments proposed are well-designed. There is confidence that useful information will be garnered from these studies. The one major weakness lies in the over-expression experiment shown in Figure 3D, where there is an almost undetectable downregulation of 37 IGF-1R. The generation of such genetically manipulated cells is critical for the in vivo experiments proposed in Aim 2. Despite this weakness, enthusiasm for this application is high.

Reviewer 3: [Score = 3] “This well-written application by Rice tests the novel hypothesis that Beclin 1 functions as a tumor suppressor…. Overall, this is an excellent proposal that presents a very interesting model that is soundly reasoned. However, at present it is still not clear whether this is truly an autophagy independent mechanism. Further, other autophagy-independent mechanisms of Beclin 1 that have previously been described such as effects on BCL-2/apoptosis are minimally addressed.”

Reviewer 4: [Score = 4] “The hypothesis are sound and the preliminary data is abundant. However, my enthusiasm for this proposal was dampened by the somewhat scattered manner in which it was presented. The approach section was confusing and concepts introduced were not properly addressed in the introduction. Finally, the lack of a sufficient diagrams of models makes it very difficult to track the varying aspects of the experiments to determine whether the expected results were sound.”

This aside, the authors note one key limitation: All of these grants were funded, so the "obviously bad" grants that might have generated more agreement were not included here, and they didn't look at whether disagreement was lower for more "obviously good" applications, which is what the "messy middle" model would predict. I would also add that the disagreement metrics they used are not trivial to interpret:

One of these is Krippendorff's alpha which seems more intuitive to me (Similar to Cronbach's alpha in psychology). It goes between 0 and 1 where 1 is maximal agreement. The value they got is 0.024 with a CI that makes it compatible with zero. As an example, suppose four reviewers give scores [3,3,3,4] to a proposal. This seems like they are in the same ballpark overall, but in that case Krippendorff's alpha would be -0.22, as calculated by the R package irr which seems to be what the authors used, indicating systematic disagreement!. This doesn't seem right, these ratings are sort of the same and yet we are getting a negative score! The same is true of the other methods, so this paper doesn't really tell us that much. If we assumed for example that reviewers say a score that's equal to the "true" score plus +/- 1 noise (So the average of four reviewers will be close to that true score) this seems like as a group they will estimate the right score, and even an individual reviewer will be close to correct. Yet, Pier et al.'s methods would say there's lots of disagreement! In the Appendix I have a slightly longer example of this.

Though in the context of journal (not grant) peer review, it's useful to consider Baethge et al. (2013) as it is relevant for the "how to measure agreement" question. Here's the gist of it, from the principal findings:

554 reviewer recommendations on 206 manuscripts submitted between 7/2008 and 12/2009 were analyzed: 7% recommended acceptance, 74% revision and 19% rejection. Concerning acceptance (with or without revision) versus rejection, there was a substantial agreement among reviewers (74.3% of pairs of recommendations) that was not reflected by Fleiss' or Cohen's kappa (<0.2). The agreement rate amounted to 84% for acceptance, but was only 31% for rejection.

Some papers have suggested that reviewers can be trained to make them agree more, by making clear what the criteria for judging are. Sattler et al. (2015) took 75 professors and had them review grant proposals before and after watching a training video they produced, substantially increasing their agreement on what grants were worth funding.

If one given reviewer doesn't have a perfect view on how good some work will be, what about when you put many together? Under the Condorcet jury theorem, adding more reviewers should yield more convergent scores. Forscher et al. (2019) examine precisely this in the R01 grant context and fund that this is true, and that the minimum number of reviewers to get a good score is around 10. Whereas the authors say NIH uses 3 reviewers, it's 3 reviewers that read and discuss the proposal at a study section, but then the entire study section gets to assign scores to the most promising proposals, and there can be 20-40 scientists in a study section; moreover they get to change their score based on the discussion.

Conclusion

I think the evidence does not merit the conclusion that pre-grant peer review is as useless or as stifling of innovative work as some have voiced. But it does not strongly support that peer review is the best that we can do either, far from that. Just because it's the default it shouldn't be privileged. What should be done is testing. The NIH (Or one of its institutes) could decide to randomly assign submissions to one of a number of buckets:

• Process as usual
• Not even assess for soundness, just randomly pick a number of them
• Use past bibliometrics scores (past success) as weights in a random choice among all the grants
• Peer review just for basics scientific rigor, then randomly pick among those

Or anything else really, and then compare outcomes a number of years after.

During the discussion above, most of the papers there use some form of citations as a proxy for "good or impactful work". But citations are imperfect. Scientists cite work for all sort of reasons. Citations may be critical, or a paper may be cited a lot because it's a review, not because it says anything novel, or a paper might be cited due to deference to a leading figure in a field. When we ask "Does peer review 'work'", defining what that 'work' should be is hard. From Gallo et al. (2014):

However, a central question in scientometrics is how best to evaluate research, as many metrics have considerable limitations or are influenced by a variety of factors that are not associated with research quality or scientific impact (Nieminen et al., 2006; Bornmann et al., 2008a; Hagen, 2008; Leydesdorff et al., 2016). For instance, citation levels are influenced by the number of co-authors, journal prestige and even by whether the results are positive or negative (Callaham et al., 2002; Dwan et al., 2008; Ioannidis, 2008). Moreover, for biomedical research, the societal impact of a study is not only measured in its contribution to the knowledge base (Bornmann, 2017), but also in actual improvements to human health; however, linking the influence of individual works to the development of new therapeutics is problematic, as they rely on large bodies of work through their evolution from bench to bedside (Keserci et al., 2017). Nevertheless, as the recent Leiden manifesto points out, performance measurements should “take into account the wider socio-economic and cultural contexts,” and that the “best practice uses multiple indicators to provide a more robust and pluralistic picture” (Hicks et al., 2015).

What would be a better metric of good work? Patents offer an alternative and some of the papers above use them: Patents are closer to representing putting the relevant knowledge to use, and to the extent that science is valued because of its practical applications, patents would be capturing that. They would fail however to capture more basic research. Recent work using PCR does not cite the original PCR work, it's just assumed as broadly known.

[Edit 2020/01/10] A caveat to the analysis above is that it is limited to projects that are proposed in the first place, and then funded or not. But it can be the case that researchers abandon promising risky ideas before even proposing them, for fear of what that'll do to their careers. The physicist Lee Smolin says in his book The Trouble with Physics:

“This system has another crucial consequence for the crisis in physics: People with impressive technical skills and no ideas are chosen over people with ideas of their own partly because there is simply no way to rank young people who think for themselves. The system is set up not just to do normal science but to ensure that normal science is what is done. This was made explicit to me when I applied for my first job out of graduate school. One day, as we were waiting for the results of our applications, a friend came to me looking very worried. A senior colleague had asked him to tell me that I was unlikely to get any jobs, because it was impossible to compare me with other people. If I wanted a career, I had to stop working on my own ideas and work on what other people were doing, because only then could they rank me against my peers.” [...] “A few chapters back, I suggested that there are two kinds of theoretical physicists, the master craftspeople who power normal science and the visionaries, the seers, who can see through unjustified but universally held assumptions and ask new questions. It should be abundantly clear by now that to make a revolution in science, we need more of the latter. But, as we have seen, these people have been marginalized if not excluded outright from the academy, and they are no longer considered, as they once were, a part of mainstream theoretical physics. If our generation of theorists has failed to make a revolution, it is because we have organized the academy in such a way that we have few revolutionaries, and most of us don’t listen to the few we have.”

Appendix: What Krippendorf's alpha does

An example with a few more papers

If we run an analysis like the one in the paper we get an alpha of 0.362 indicating a lot of disagreement whereas, on my view, all the papers are reasonably rated with the exception of paper 3. If you take "Reviewers disagree" as the difference between the maximum and minimum rating being greater than 2 say by this metric 75% agreed.

require(irr)
papers=matrix(c(3,4,1,1,1,4,3,9,2,2,4,5,7,1,3,3,3,2,1,1),nrow=5)
kripp.alpha(t(papers),"ordinal")
> kripp.alpha(t(papers),"ordinal")
 Krippendorff's alpha

 Subjects = 5 
   Raters = 4 
    alpha = 0.362