By most available criteria, the United States is still the undisputed leader in the performance of basic and applied research (National Academy of Sciences, 2007)

Since 1969, US-based scientists have won more (Science) Nobel Prizes than the rest of countries put together. While this metric is one among and others, especially those measured more recently, don't show such an overwhelming dominance of American science, the general story is clear.

A book I just finished reading, Markets, Minds, and Money tries to explain why. The explanation from the book, briefly, is that the American academic system has a free-market orientation that other countries lack. Whereas Europe, the author claims, rigidly imposes a centralized curriculum from the top down and tries to distribute funds evenly across regions within Europe and across nations, the US lets the most productive scientists get more resources even if this leads to an extremely unequal funding distribution (Which, if the Newton hypothesis is true, is actually a great thing).

One could however try to point to other factors that explain the success of the US, and the author has considered some of these alternative explanations. For example, perhaps the US is such a science powerhouse because it was the destination of a good chunk of German (after WWII) and Soviet (after the collapse of the USSR) scientists. That surely contributed but the US was already on its way to scientific preeminence before that: US Academia began to eclipse the rest of the world by the 1920s:

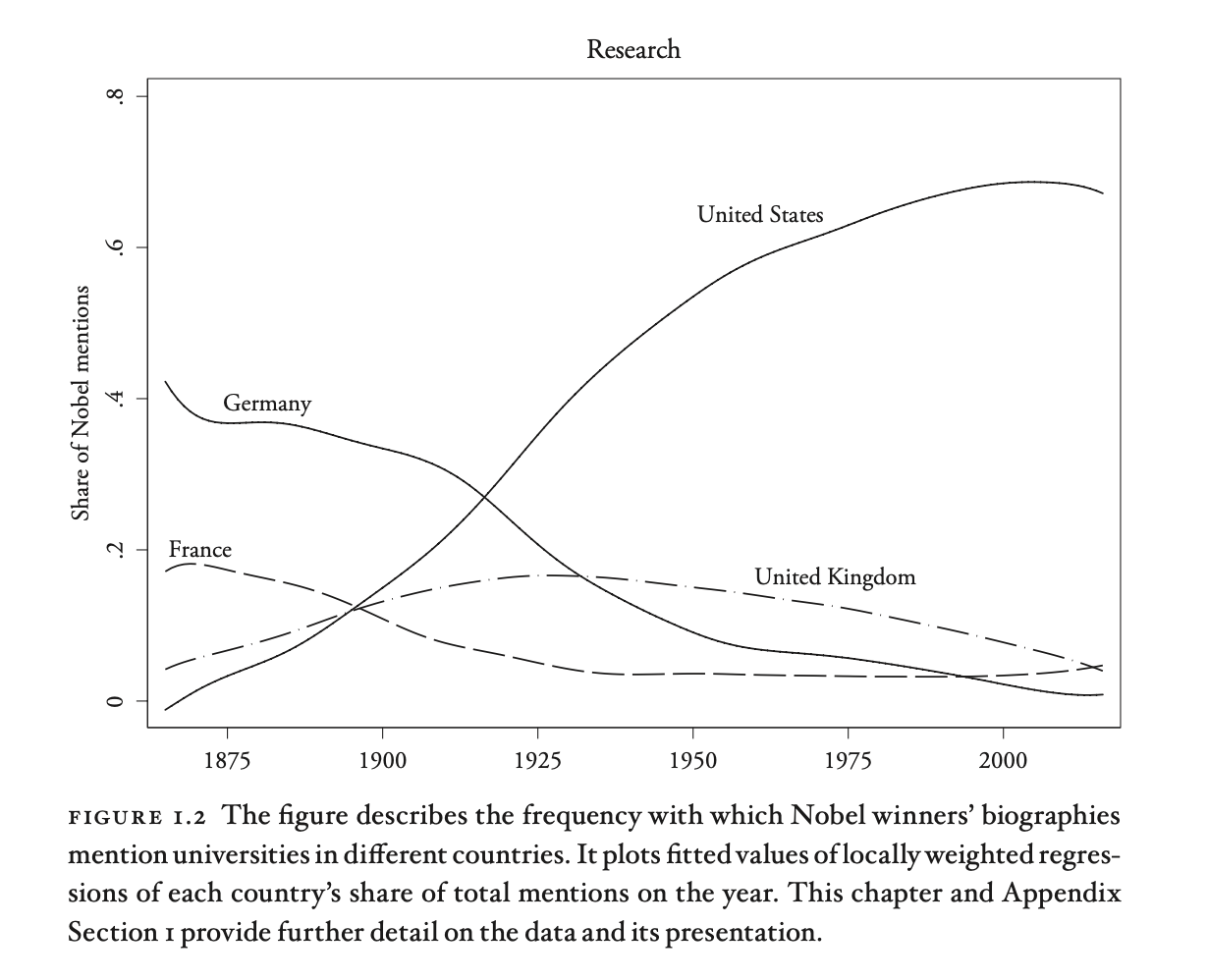
This is different from Nobel Prize winners being American or US-based foreign scientists, that started before WWII, and then got an additional boost by attracting top global talent:

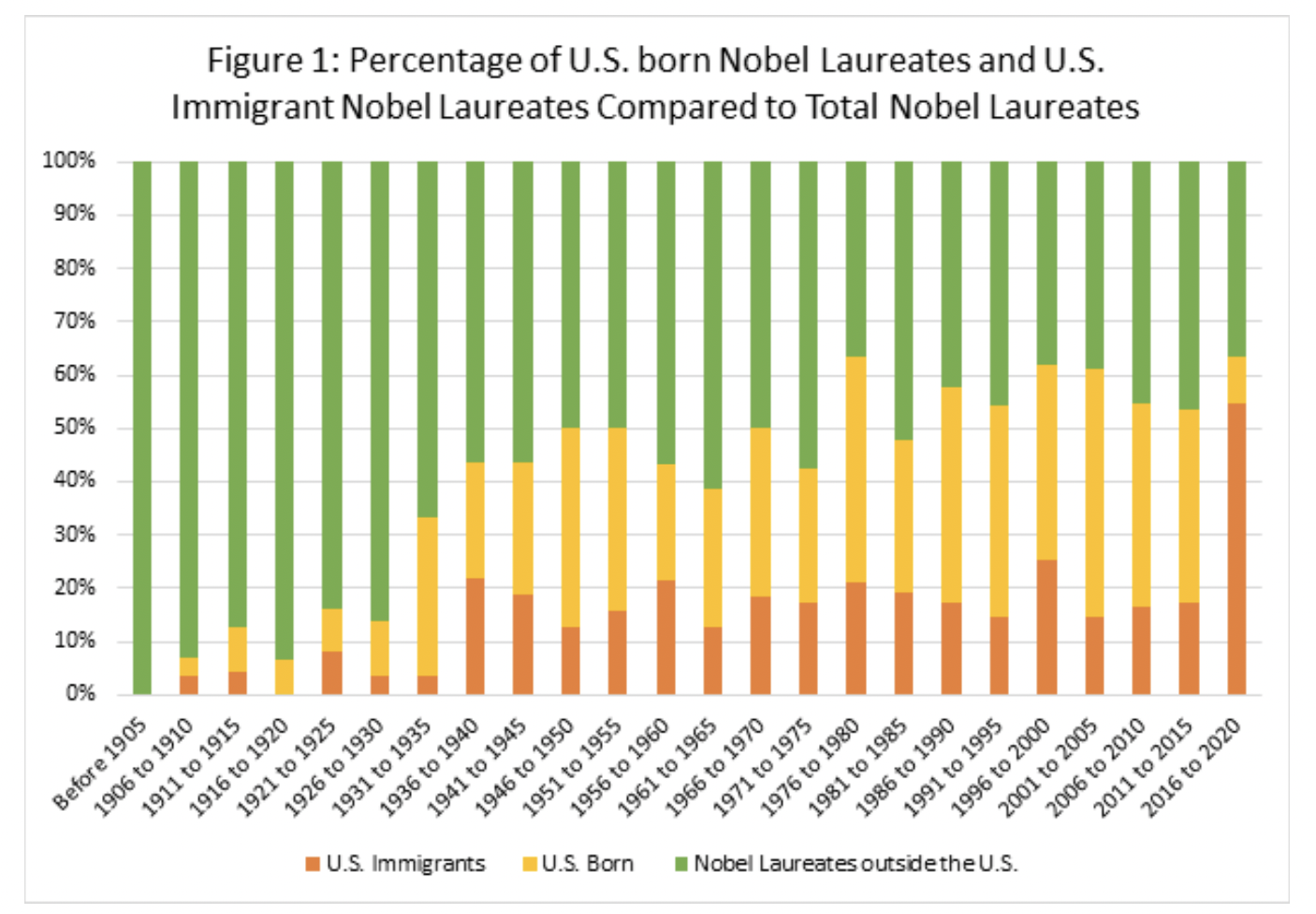
Similar, more detailed figure from here:

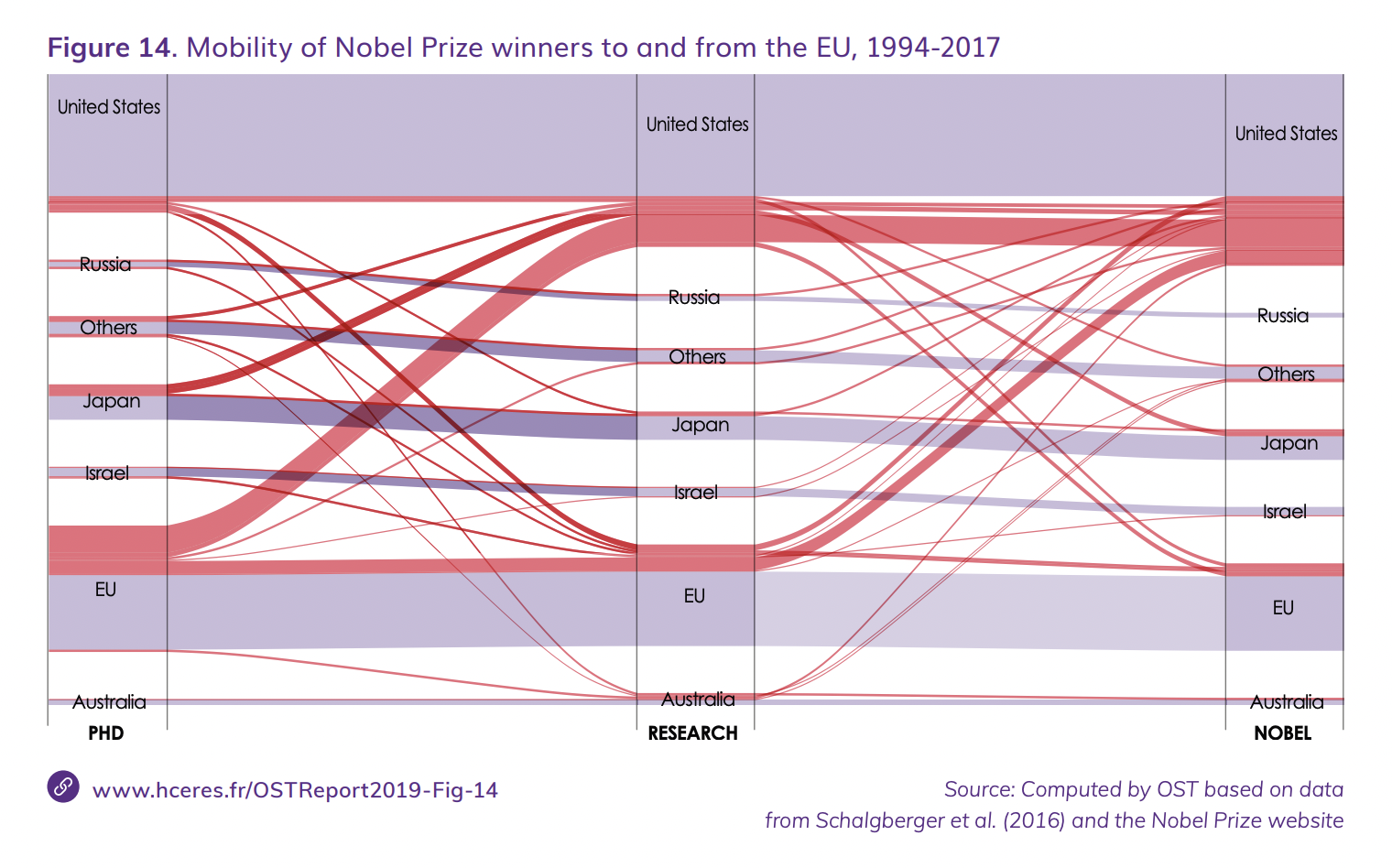
There is a chart that shows that inventors tend to migrate to the US disproportionately relative to other countries. I couldn't find a similar one for scientists broadly (other than Nobel prizes), but I wouldn't be surprised if it looks very similar:

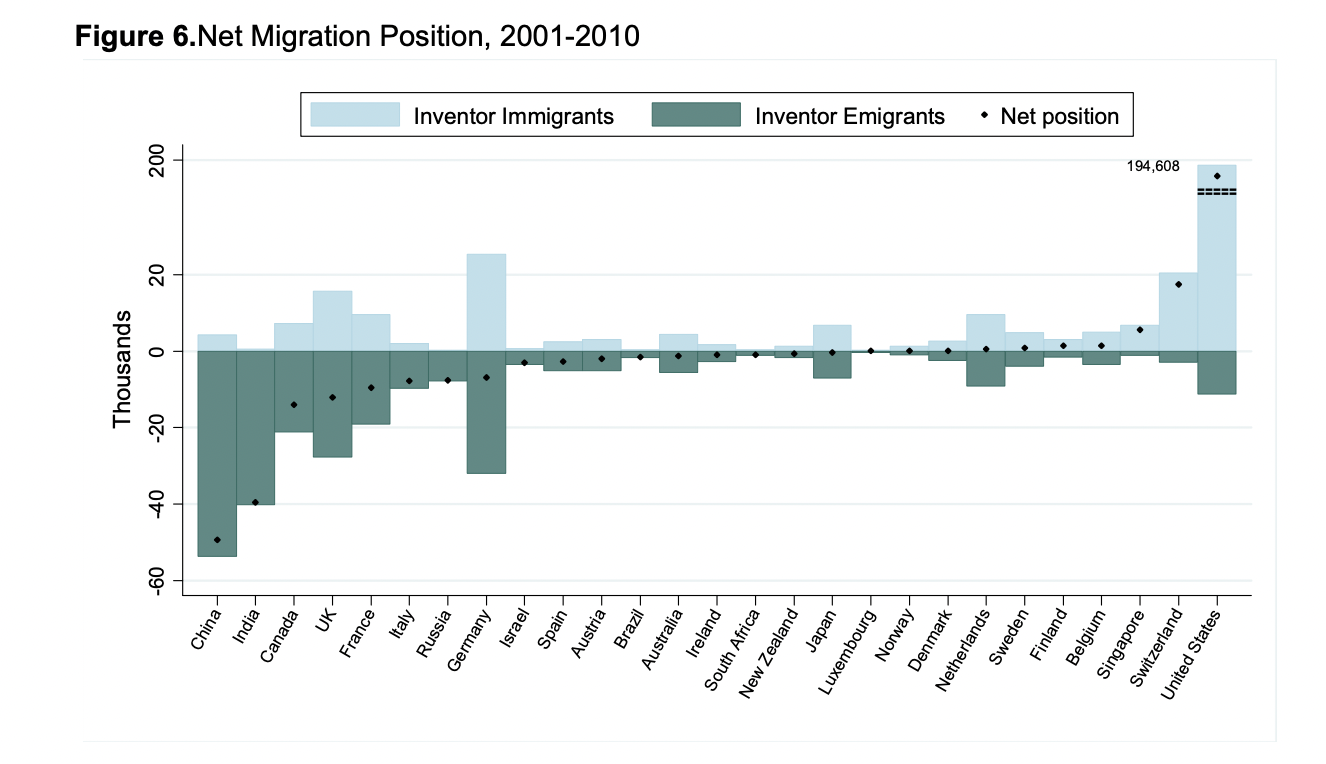
The reason why we see this could be an intrinsic advantage of the American system, the free-market orientation described in the book (more opportunities to do the research the scientist wants?), but it could also be other factors. Suppose for example that the US transitions to a European-style (German-style?) scientific ecosystem. Leaving everything else unchanged it would still have two factors that may explain the patterns observed: population and wealth. Being able to finance more numerous and more expensive experiments and pay higher salaries alone could explain a chunk of US success.

The first one of these factors (wealth) was not addressed in the original paper; Michael Nielsen was thus doubtful (see tweets here) about the overall result (It's something one should totally control for!). I thought that perhaps the book would have considered this. While they tried, I don't think they did satisfactorily.

The appendix of the book considers this and has some numbers normalized by income:

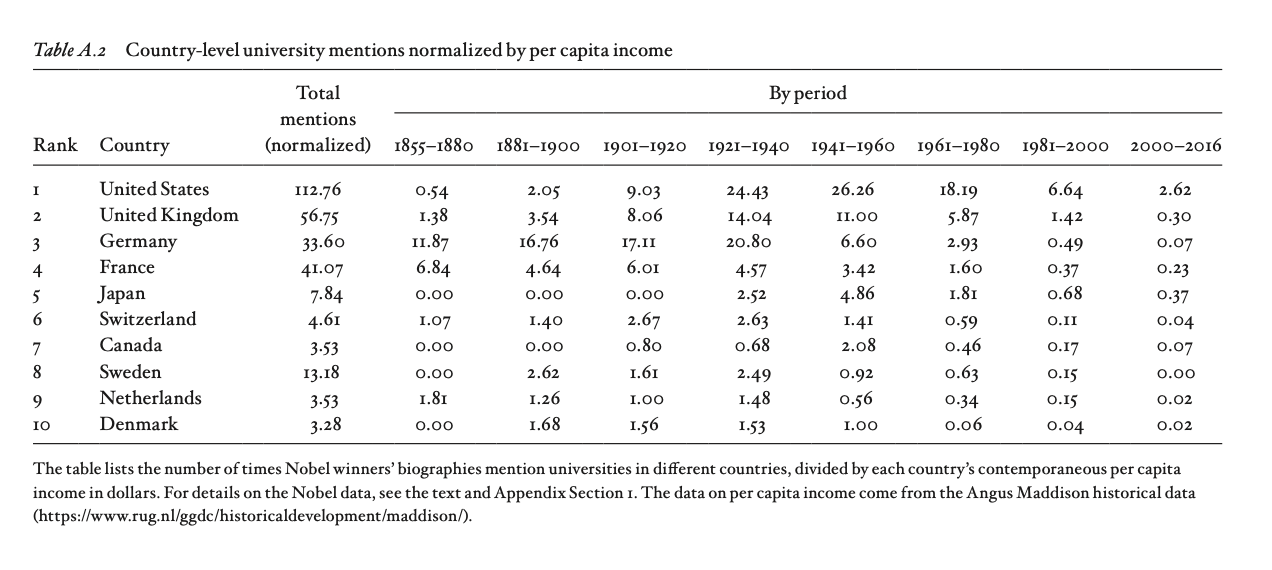
Here one'd want to perhaps control for salaries in higher education instead though. With that caveat, the pattern holds.

The same is true, to a lesser extent, if one controls for population;

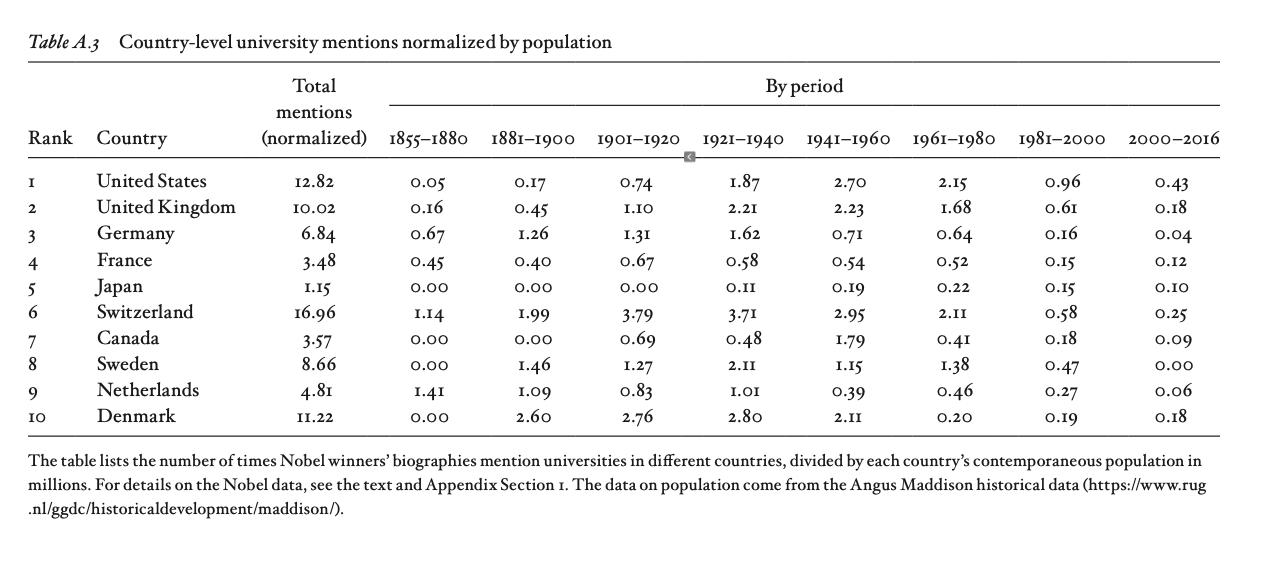
The UK manages to remain competitive to some extent whereas France and Germany gradually fall in the rankings. Even here, we don't want to control by population in general, rather we'd like to control for the number of scientists in each country; however, the number of scientists is endogenous to the performance of the scientific system itself: success will attract more success. With that caveat, the image below accounts for researchers, and it largely matches Urquiola's story, with the US and the UK (Which he says has a similar academic setup) leading (set aside the countries with a small number of Nobels awarded), the one interesting outlier here is Israel (at the PhD level) but it seems a lot of those Israelis end up working in the US.

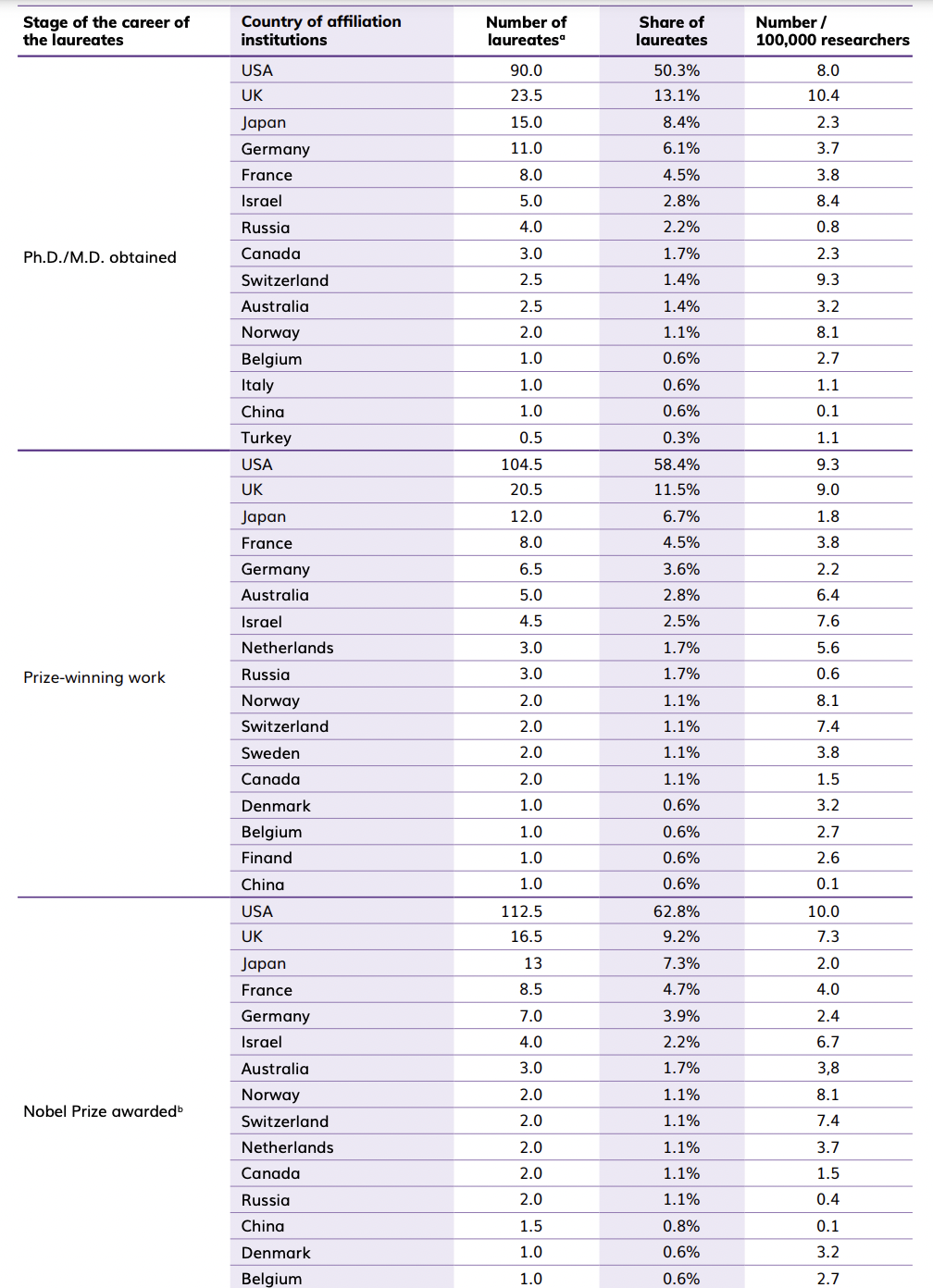
What if one controlled for both though? Crude measure as it is, in economics in general there's a notion of productivity above and beyond inputs (Total Factor Productivity). Here we could define a simple model where scientific productivity (as proxied by total citations, or just Urquiola's own mention-based metric) depends on the product of R&D spending and the total number of researchers, times a residual. The evolution of that residual would get us productivity. Whereas it seems plausible that the way the US academic system is structured can act as an advantage, I'm not so sure that once we control for immigration and more funding available, the US' lead continues to be dramatic. This should be truer of fields that require more funds.

Perhaps, it could be also argued, explaining the success of the US and the fact that its rise starts before WWII requires multiple factors. First, there could be a simple story of catchup, where US science was developing to match Europe, explaining the initial boost, then we would add the effects of WWII on European science as a one-off effect to which we would then add the trickle of researchers immigrating to the US since then.

China

Something that is not discussed much in the book is the rise of China, though this is acknowledged:

Because universities cannot be mentioned in winners’ biographies until they win, our measure penalizes “up and coming” schools. For instance, in recent decades, countries like China and South Korea have invested in their universities. To the extent that these are now training outstanding students, they will take years to show up in Nobel biographies. That said, our re- results for recent decades match up well with rankings that use bibliographical data likely to reflect progress more rapidly. In addition, this book’s focus is not on recent developments, but on the rise to dominance of American research universities.

Fair enough, but if it turns out that a) China's academic productivity is rapidly increasing and b) The Chinese academic system is not free-market oriented, then the thesis of the book is much weakened. At best, it would say that during a particular period in history, the American university structure was useful. At worst, it's a vindication of the null hypothesis: That money and minds alone explain the bulk of scientific success.

Since the early 2000s, China has granted more Science & Engineering (S&E) bachelor degrees than the US and almost as many doctorates. China will soon be spending more (in absolute terms) in R&D than the US. As of the late 2000s, China produces more scientific articles than the US (but not more than the European Union). Now that China-to-US brain drain is slowing down (and perhaps over by now; though not in every field, see the case of AI) and top Chinese talent stays in China more often, we may start to see the rise of China among Nobel Prize citations as well. By various rankings, Chinese universities are appearing more often among the top universities.

So are Chinese universities matching money with minds effectively as in the US? Or sorting outsmart students? For that latter, I'd adventure to say that probably. The US' SAT seems weaker than China's Gaokao.

Has China reached a leading status in any field yet? We can't yet see this in Nobel Prizes, but that lags the actual research by decades. In AI the answer is: getting there (by top publications; but see the remark on "Best Paper awards") and no (by the count of papers accepted to leading conferences). Lots of growth hacking by Chinese researchers citing each other, but the work itself is not good?

Figure 5 of this paper shows that China has indeed been improving the quality of their research (proxied by highly cited work), but it's still far from catching up with the US; conversely it looks like if one takes the EU as a whole, then the EU is leading, more so if one adjusts by GDP.

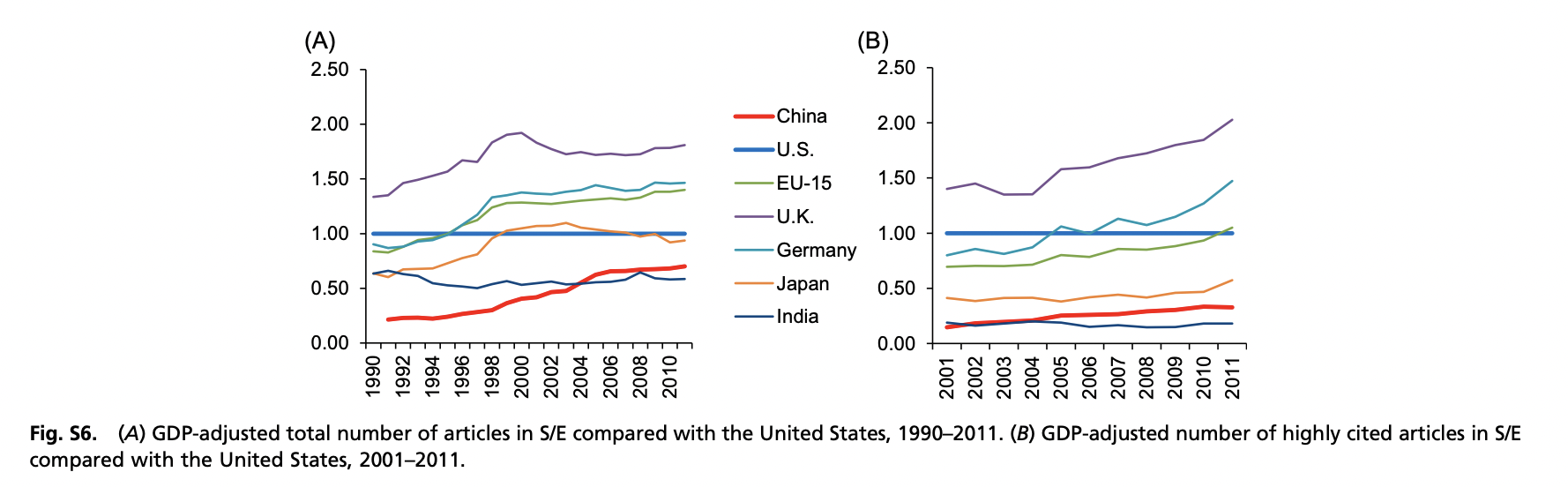
This is still compatible with the US producing the very best of work, say the EU can produce the best 10% of the work, whereas restricting that to the top 1% gets us to US leadership, and that's what appears in Nobel Prizes. A quick perusal of other Nobel Prize-type awards confirms that US-born and -based researchers get the majority of those prizes (von Hippel Award, Charles Stark Draper Prize, Turing Award, IEEE Medal of Honor, Millennium Technology Prize, the Lasker Award, or the Kyoto Prize)

France

Another interesting fact to consider when trying to explain success is that if we consider mathematics (There is no Nobel Prize for that), then France is on par with the United States; and what perhaps is the world's leading research center for mathematics (by the count of Fields medals), the Ecole Normale Superieure, is in France.

I'm of course not the first one noticing this. France's performance in mathematics is not explained by mathematics funding (A fraction of US's):

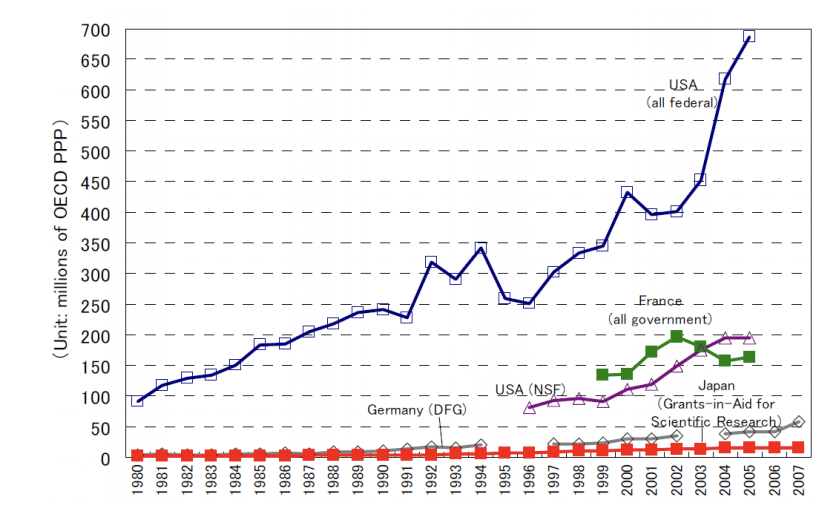
or even just population. The US publishes more papers; publications are directly proportional to the number of authors, especially in a field like mathematics where single authorship is frequent (Table 3 here confirms the idea that the average N of authors per mathematics paper is similar across countries) and this further confirms that there aren't that many French mathematicians, even historically:

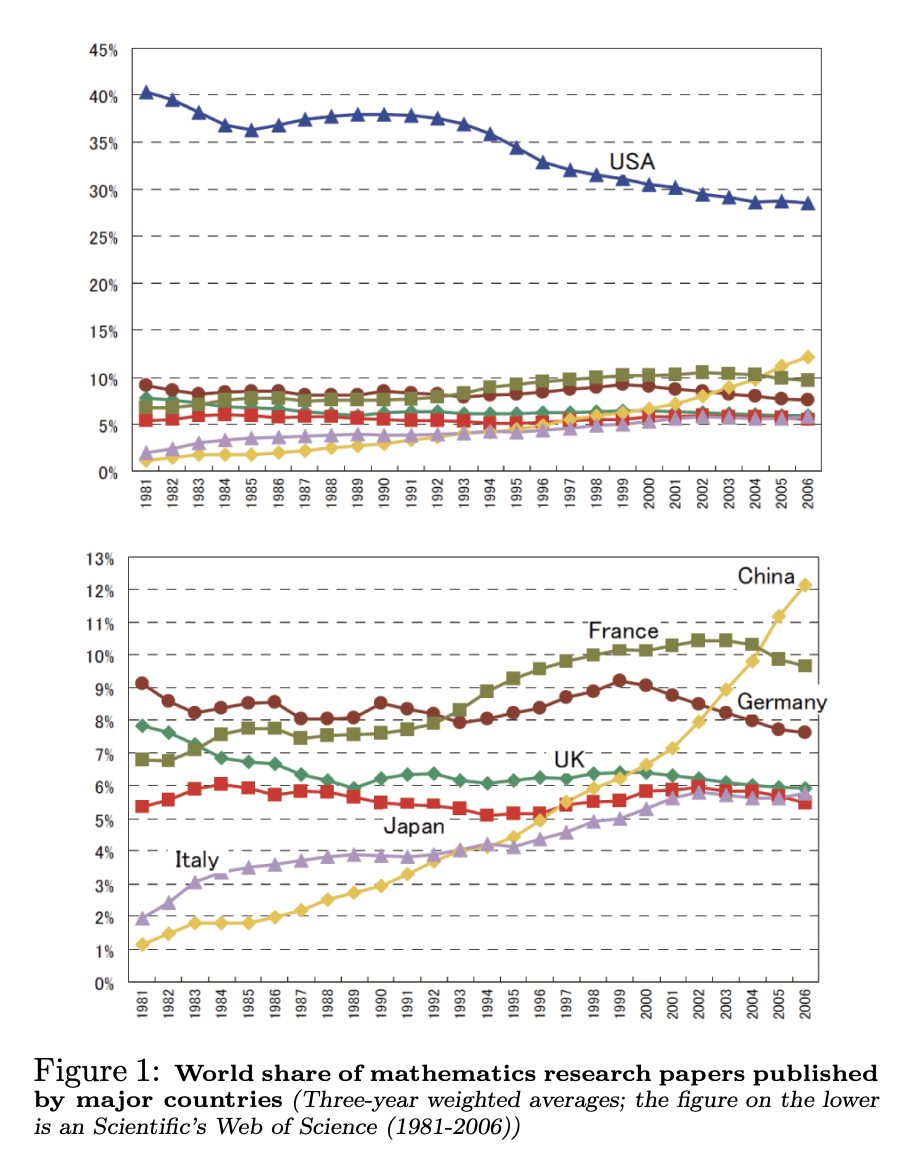
So despite the US funding more mathematicians and publishing more papers, France continues to be extremely competitive at the highest levels of mathematical achievement; implying, perhaps that either they have more top talent than the US, or they manage to nurture it better.

It gets weirder: French kids' performance in PISA maths assessments is merely average, and way behind the usual suspects (Singapore, Hong Kong, or China). France doesn't do particularly well at the International Mathematics Olympiad, with fewer gold medals than, say, Bulgaria, Vietnam, or Thailand. The first fact is easy to reconcile: what matters is not the average but the best. The latter could be explained by a lack of interest in the IMO, perhaps the best French students are busy preparing to join an Ecole Normale Superieure and the IMO is a distraction. But then again, why does China lead the IMO but is underrepresented in the Fields Medal?. Maybe the kinds of problems that one has to solve at the IMO are different from the kinds of problems that get you a Fields medal?

A culture of mathematicians

Another explanation is that France is specialized in mathematics; that a higher fraction of their researchers, and plausibly their top researchers too, specialize in maths whereas in the US those top students are more likely to go into say biomedical research or social science. This seems true, see for example Figure 29a from here, which compares the national allocation of talent (proxied by publications) by discipline relative to a global average:

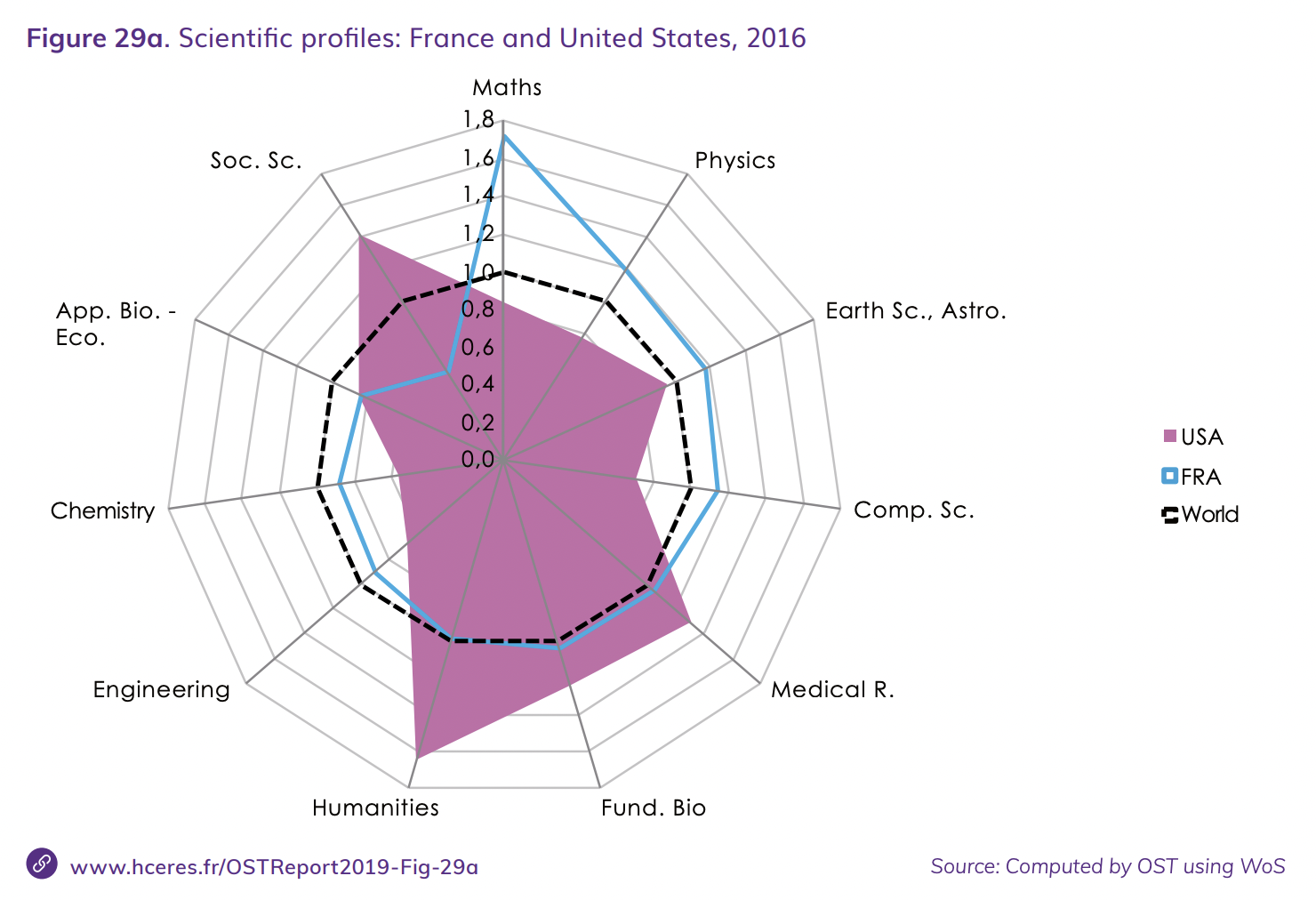
And this starts early on:

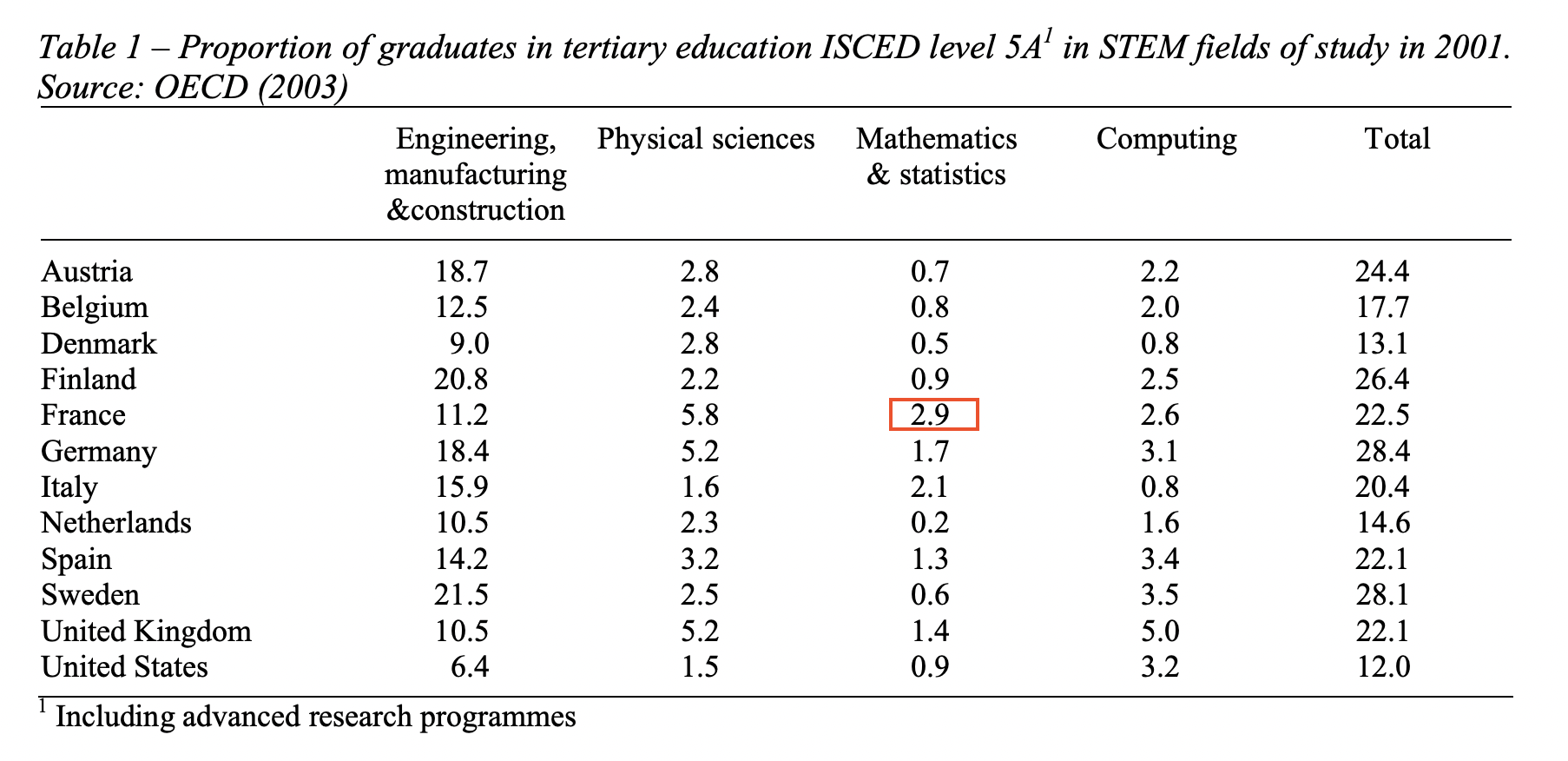
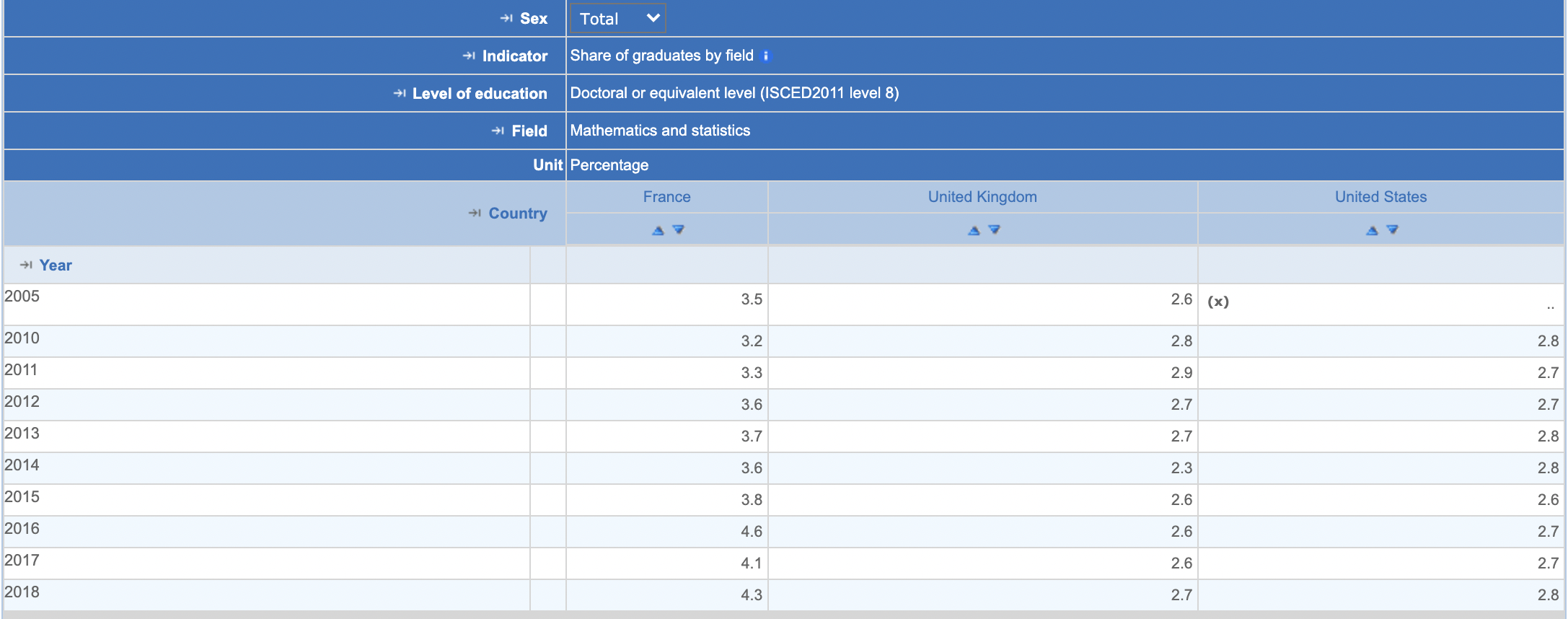
The proportion of students in tertiary education studying mathematics in France is 3x that of the US if one pools together BScs, MScs, and PhDs. That drops to 1.5x in France if one considers only PhDs (See here). Comparing across countries, the US looks relatively stable, whereas the proportion of PhD students that choose to specialize in mathematics if anything is increasing in France.

Free minds?

It's likely that to make progress in fields like mathematics one is at an advantage if one is young (for more see here). In France's ENS, PhD students and postdocs are public employees (they don't pay for their education, the State pays them; in exchange for a 10-year service commitment). Does this mean that they can be 100% dedicated to research, avoiding e.g. teaching responsibilities (Which US students have)? I couldn't quite find a source to see if this is the case, so I went to the mathematics department of the ENS and looked at postdoctoral and doctoral students to see if they list any teaching experience. Many CVs are not available but many of them do teach some classes

I find the cultural argument (mathematics is seen as a worthy pursuit for the brightest students) the most plausible to explain France. To be sure, this may also be an incentive story (France has economic support for mathematicians, but more than the US?), that's hard to disentangle from saying that studying maths is more encouraged or preferred. It could also be something about the way mathematics is taught in France, but I was not able to find online anything that would suggest that it is drastically different from elsewhere. I initially thought that maybe they emphasized memorization a lot, but that may be a universal feature of mathematics education.

Conclusion

Can we square Urquiola's theory with the evidence above? Not so sure. How could the theory explain France or the rise of Chinese universities? Perhaps he may respond by saying that mathematics is a special case, one doesn't need a lot of money to do math, just a salary and paper whereas for more expensive endeavors maybe it pays to concentrate funding more? The book is trying to explain why the US succeeded at getting more mentions in Nobel biographies than Europe, but I don't end up all that convinced that this is what explains the bulk of US success, current or past. Doing that would require controlling for fraction of spent R&D and the number of researchers (native and foreign), preferably by field.