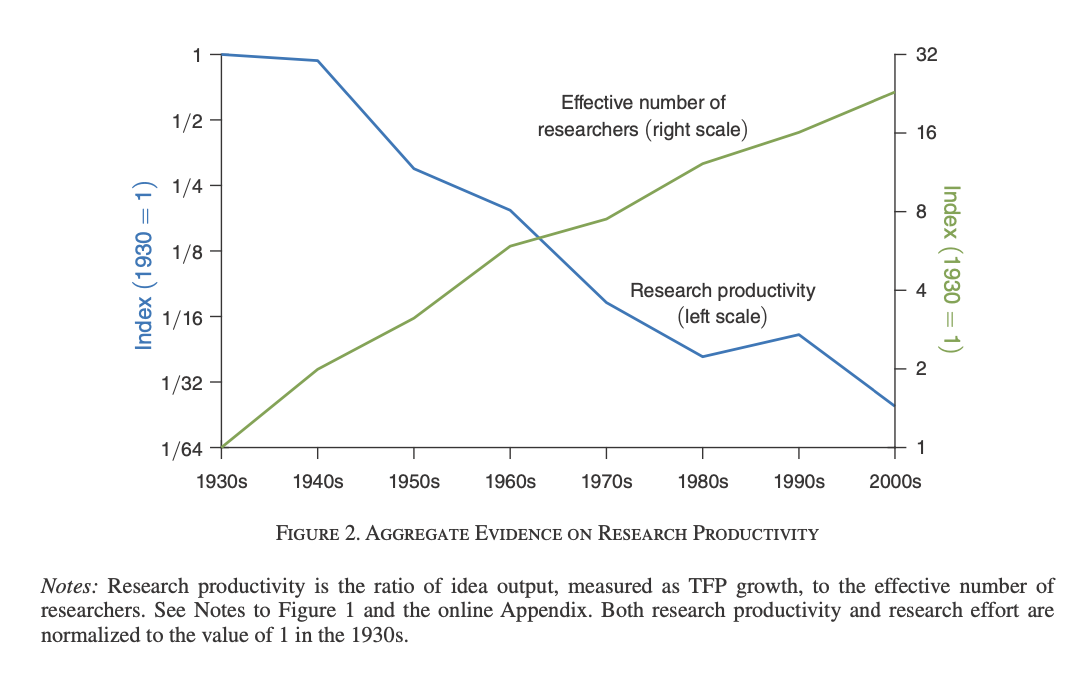
Are ideas getting harder to find?

Are ideas getting harder to find? (2020) by Nicholas Bloom, Chad Jones, John van Reenen and Michael Webb repeatedly pops up in discussions of technological progress, the great stagnation and related topics. They take a different angle from the usual, rather than debating whether there is stagnation or not in a range of metrics (Like TFP, Moore's law, crop yields), they instead opt for taking the optimistic view (That those metrics are advancing as usual, in some of their models) and calculate instead how much does it cost to get there by various means (like R&D expenditures). The result: The US is spending more to get the same level of yearly progress, hence ideas are indeed getting harder to find. And not just the US, a later followup (Böeing and Hünermund, 2020) applying the same methodology found the same thing in Germany and China looking at a panel of firms.

I was in a dinner once where at some point I was asked if there's a great stagnation, I answered that that's the wrong question to ask. Whether ideas are getting harder to find is in the came category. It's too high level to be operationally useful. Given the goal of accelerating progress, one has to look at each field and see what the roadblocks facing the field are, and how much would it cost to remove them, for what return. This assessment is the same regardless of whether we regard a field as stagnant, accelerating, or in a business as usual stage.

So what does the paper do? They assume that $$\frac{\dot{A_t}}{A_t}=\alpha S_t$$

where \(\alpha\) is a measure of research productivity, while \(S_t\) is the number of researchers (with some adjustments) and \(\frac{\dot{A_t}}{A_t}\) is growth in TFP, which relates to new ideas. You are probably thinking various things:

1. The relation is not linear, maybe one should introduce a correction term that accounts for reduced productivity due to duplication of research. They thought about that: that weakens the result but it still shows up)
2. What R&D should they measure. Good point! The authors admits that this is tricky, and the reason why they didn't chose trickier case studies as the human genome project or light (A classic example from Nordhaus). But even then there may be issues. Later I show that no matter what R&D metric you choose, the result is the same.
3. The equation assumes exponential growth! Well they do, hence they concede that the paper may well be "Is exponential growth getting harder to achieve?". In many sectors this is what you see and I won't object to using an exponential model for Moore's law. But as I remarked elsewhere, some technologies improve (at least for some times) superexponentially, and others linearly. In any case as I will be focusing on Moore's law I won't quibble much with this. I think exponential, or rather logistic, is a reasonable model for growth in most cases within a given paradigm.
4. The authors also consider the case where productivity in a given field gets stuck yet new fields get invented that allow aggregate productivity to continue to improve (The model I had here where exploiting a paradigm is like mining, you need to keep opening new mines as each mine has finite knowledge). This is why they look at the US as a whole. This is reasonable.
5. You may also think that the number of researchers is artificially inflated because academic institutions keep getting flooded by lowly paid grunts that do not really contribute. One could make this case for the aggregate economy but not for the Moore's law case as they consider exclusively the semiconductor industry.
6. Another choice they make is to deflate R&D expenditures by the prevailing wage rate. In the semiconductor world a lot of R&D plausibly is capital expenditures, but they also address this in the "lab equipment section". Later I use CPI as a deflator and the result, once again, is unchanged.
7. Or you may think that their assumption that "if expanding research involves employing people of lower talent, this will be properly measured by R&D spending." because better researchers are paid more. This is an interesting assumption! In Academia this may not be true, the grifter that got into Academia by inertia and just wants to stay afloat gets paid as much (And not much) as the bright one who is inventing the next iteration of batteries. At the very top sure, top PIs may get extra money from patents, board seats, or their own startups. But! Remember, they looked at industry, this critique applies for their aggregate numbers, not the Moore's law one. Surely industry imposes some discipline on semiconductor companies, forcing pay to go more in line with productivity?

Moore's law is a good example they discuss in the paper. It's well documented, the semiconductor world is not that big so it's possible to know who is up to what, and in the paper they consider the most optimistic case of the law: transistor count. If you remember from my post on Moore's law, the diagram at the end shows that indeed transistor count seems to be rising exponentially, with everything else slowing down (But still growing!). So if they can show that even with transistor count research productivity is going down, then a fortiori for other ways of interpreting Moore's law (Like single thread performance or computations per dollar), those will also show a slowdown. All the data they used is available in the online appendix so we can look at it (I got a copy here with some of my own calculations in Sheet 1). What does R&D expenditure look like, both for semiconductor companies and companies supplying tooling to said companies like ASML or Trumpf. Out of all the semiconductor companies, should you include everything in your analysis? The authors try some variations (Table 1) including just Intel, or Intel+AMD. Including Intel dominates the results, drastically driving down productivity growth.

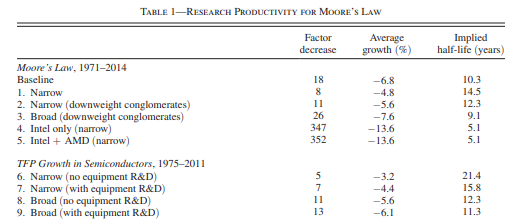
They don't use this number in the final table, they use their baseline result which is around the middle of the other estimates. But this immediately seems interesting: Could it be that it is Intel that is driving down the results? What if it's not that ideas are getting harder to find, but that some companies are getting worse at it? This may not be a general explanation. In physics, I do think the low hanging fruit theory fits well the data. But not here. This is what expenditures look like (Numbers are not adjusted for inflation, but serve for relative comparisons)

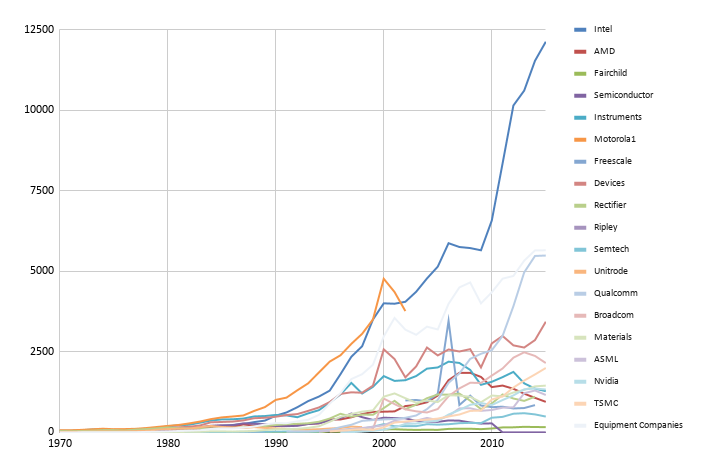
Indeed Intel by far dominates the R&D expenditures landscape. The next line is the sum of all the equipment companies. We then have Qualcomm and then Analog Devices, then Broadcom, and then finally TSMC. Bunching together all these companies seem questionable. A foundry and Broadcom? Has Broadcom ever put a chip on the Moore's law chart? Has Analog Devices?) Where's AMD? Where's NVIDIA and their stream of state of the art GPUs? Why is ASML in the semiconductor category instead of in the semiconductor equipment one? AMD just launched this year the best desktop processors there are (Along with Apple's M1). We just got the RTX 3090. There's also Apple's astonishingly great M1 but teasing out Apple's semiconductor R&D from other R&D is harder so I won't be looking into that here.

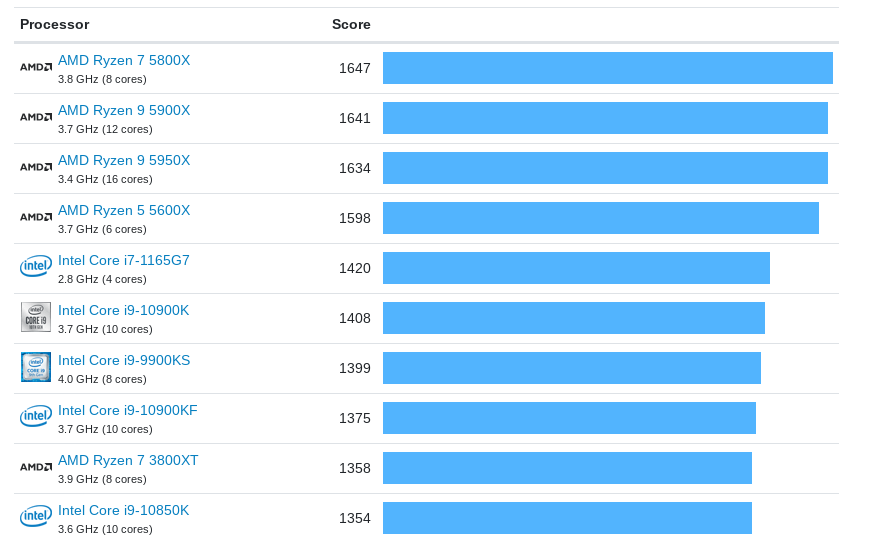
From 1996 to 2015, Intel increased their R&D by a factor of 6.7. AMD did so by 2.36. AMD is not just AMD, they now make their chips at TSMC while Intel is an integrated fab+design shop. So let's do the following: Let's take ASML+the semiconductor equipment companies, add that to both AMD and Intel, then add TSMC to just AMD, and compare those two numbers. We get this:

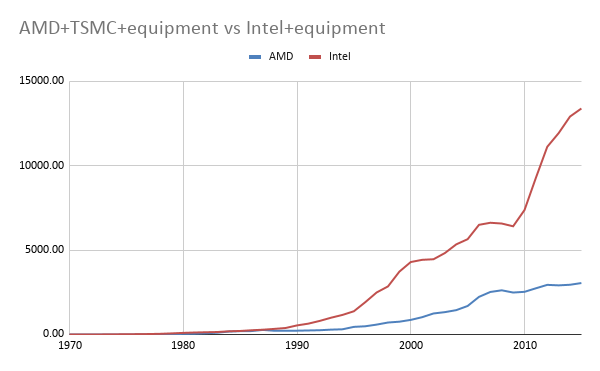
So it looks like Intel has been spending a lot quite recently, and not so for AMD. Maybe AMD started spending after this and that's where we got Zen3 from? But no, AMD's own R&D has stayed flat. Anecdotically, going by my favorite metric, performance (According to geekbench for convenience), AMD has been able to go from the 587 points of the FX-4330 in 2016 to the 3562 of the latest Ryzens, an increase of 6x. Intel achieved a 1.5x improvement in the same period. Granted, one may say that Intel was a the frontier of technology until now and maybe AMD has been able to benefit from Intel's knowledge. That's fair; going forward it will remain to be seem if AMD R&D will rise to Intel's level and beyond. But for now the fact remains: AMD has been able to improve their chips substantially more per $ than Intel. You can see the same broader point with some charts here using different tests. I am not doing here transistors but single thread performance as it's an easier figure to come by, and reflects more faithfully what the industry is optimizing for (Besides thermal performance).

One may object to my analysis that I'm just throwing away everyone else, has all the money that others companies put into semiconductors done nothing? No, it has led to their own chips and designs, but it's plausible that at the bleeding edge of design indeed that what the others have been doing is irrelevant. In fact if we just talk about cramming more components into less space and forget about design, then we are looking just at TSMC and the supplier companies (Or Intel plus suppliers), in which case their expenditure increased 15x since 1995 (When the TSMC time series begins) to 2015, a figure closer to AMD's cost increase than the Intel's increase. Moore's law implies a 35% increase every year in transistor count; so in that period that's 404x more transistors.

This all is, however, not exactly what the paper does; additionally we have to take the expenditure and divide by the wages of highly skilled labor to account for inflation. When doing comparisons as I have done the denominator does not matter (So the seeming inefficiency of Intel which drives down the industry's research productivity is still there). But when redoing the calculation of absolute changes in research efficiency it does. The corresponding file is RNDSalaries.mat (The legitimacy of using US wage data to deflate companies in Taiwan and Europe is left as an exercise to the reader), and from there we get that the change in effective researchers was of 8.11 which puts us in the narrow estimate from the paper: Their result stands.

What would it take for ideas not to be getting harder to find? Well, for one in a simplified model where the only R&D costs is researchers' wages, then the number of researchers must be constant!. In a model closer to the paper where we require that $$\tilde{S_t}=\frac{RD_t}{Wage_t}=\tilde{S_{t'}}=\frac{RD_{t'}}{Wage_{t'}}$$

$$\tilde{S_{1995}}=\frac{81.16}{48450}=\tilde{S_{2015}}=\frac{RD_{1995}}{92898}$$

So the 2015 R&D expenditure would have to be 155M$ instead of 1263M$, ~8.11 times less. Either 8.11 less money, or the same researchers, that's the conclusion from the model. And this is in a more optimistic case (Where I am only counting TSMC and manufacturers). The numbers do not go away if we instead deflate R&D by inflation instead of by reserachers wages. Recall, the TSMC et al. expenditure increase was 15x since 1995 to 2015. In that period, the cumulative rate of inflation was 55.5%, meaning that $1 in 1995 is ~ $1.8 now. So the actual expenditure increase would have been 15/1.8=8.33, roughly the same figure we get if we use wages.

One may also retort with: Oh but chip companies are worried about power efficiency and other things. Yes, but that's a design issue: I have chosen companies that do not design semiconductors, just make them (TSMC et al.) to separate between cramming transistors and designing how they will be arranged.

So to recap: Regardless of how one deflates the numbers, or which firms one takes for the calculations the results hold. Given the broad class of models that underlie the paper, I think there is no plausible slicing of the data that yields constant productivity. So in the same way as Bem's psychic ability meta-analysis the paper could be taken not at face value implying that research productivity has gone down; rather one could conclude that we are doing fine historically and it's the models that are wrong. Think about it: This is not about science changing in 1970 or science doing better in the 1930s, the trends look relatively constant for the aggregate TFP and researchers calculations. Science has always been like this. Or so it seems from the data in the paper, I'm not saying it's all fine!:

Scott Alexander pointed out as much:

constant progress in science in response to exponential increases in inputs ought to be our null hypothesis, and that it’s almost inconceivable that it could ever be otherwise.

This is alternative 3 from this list he gives of potential explanations for the observed data:

1. Only top researchers produce productivity-raising ideas; if so increasing researcher count beyond those elites is inefficient.
2. The current academic system is an order of magnitude worse than the one from times past at producing useful research
3. We've picked the low-hanging fruit and it gets progressively harder to keep picking it. (Scott's preferred explanation; Matt Clancy points to a sub-variant of this, that these new ideas require harder work in the form of learning more than before)

GDP growth is exponential, as is population growth, as well as (for successful companies) market capitalization. That R&D expenditures increase exponentially is no surprise. The worry would be if R&D expenditures become a large share of GDP but that seems a very remote possibility right now.

One may be tempted to just go ahead and say that the right model should be something like what the authors suggest, where indeed the growth of "ideas" goes down as we already have lots of them in stock, a semi-endogenous model that looks like:

$$\frac{\dot{A_t}}{A_t}=(\alpha {A_t^{-\beta}})\cdot S_t$$

but why would that be: Yes, the next step is harder in absolute terms: CERN is more complex than the Curie's lab. But our tools and technologies now make it easier to build more complex tools and attempt more complex projects: We are not attempting to build colliders with the same means available to the Curies, now we have computers and better materials.

Why would it be the case that the difficulty of the projects has to grow faster than the capacity of the tools we have to attempt them? I don't have a good explanation yet!

But in any case I think it's more practical to study each field and see what's going on with it. As hard as it sounds, I think "How promising or healthy" a particular field of science or engineering is easier and more practical to answer than abstract theoretical questions about the necessity of progress curves to be shaped in a certain way. Knowing that US TFP requires more and more resources to keep going does not immediately lead to a solution, but knowing what is preventing airplanes from flying faster does lead to solutions. A worthy task for any Progress Studies researcher!