On the constancy of the rate of GDP growth

[Epistemic status: Highly likely]

Why is GDP growth in the US so oddly constant, asks Patrick Collison.

If you look at log US GDP over the past 150-or-so years, it is very weirdly smooth. Why? What determines the slope? Would it be correct to conclude that "almost nothing will affect the economy over the long run"? This phenomenon may even extend back further in the US. But it's not like nothing matters; GDP growth between countries does vary a lot, in both the short and the long run. So... what gives?

Patrick Collison (2018?)

He is not the only one:

We seek an understanding of why the advanced economies of the world, such as the United States, have grown at something like 2 percent per year for the last century. Where does the technological progress that underlies this growth come from? Why is the growth rate 2 percent per year instead of 1 percent or 10 percent? Can we expect this growth to continue, or is there some limit to economic growth?

Jones & Vollrath, Introduction to Economic Growth (2013)

As per Maddison's GDP data, RGDP per capita growth in the US has been 1.76% on average since 1800. Taking the time series from 1870 would yield 1.95% instead. (Unless otherwise noted, all data below comes from that dataset)

GDP and population

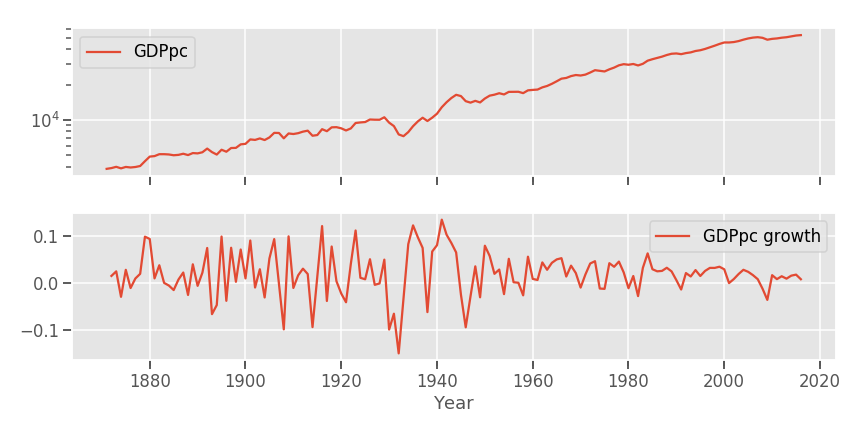
On top of this we have to add population, as simply GDP equals populations times GDP per capita. Population has grown at an average rate of, similarly, 1.47% yearly, adding up to an average rate of GDP growth of 3.54%. GDP growth indeed seems smooth:

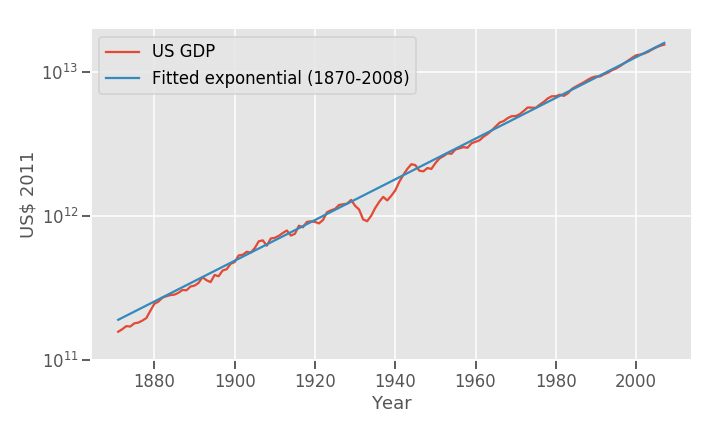
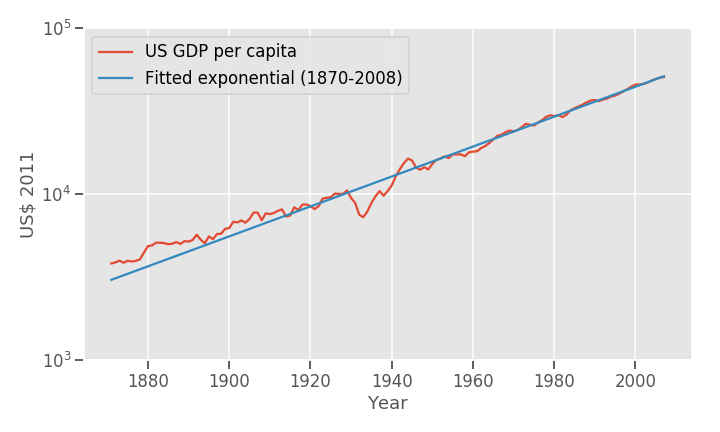
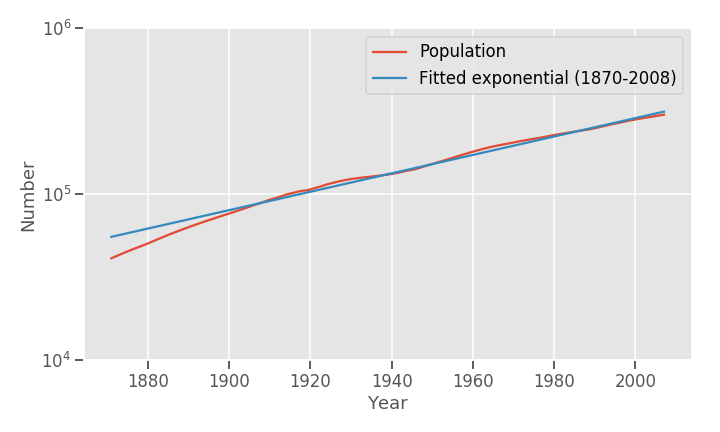
Even though growth rates are similar on average, they are not in variance: GDPpc growth rates are far far jumpier than population growth. This makes sense: There has been no wars in US soil, mass emigration/inmigration, or famines, the typical culprits for large population changes,while many GDP-altering events have happened(the boom/bust cycle, wars).

If we were interested in the rate of growth of population, instead of GDP, we could have a very simple model: Let's say that we have a bunch of people, and that they have on average of X kids per generation. That generation will eventually be replaced by a new one, so we need not worry about death rates. On a yearly basis, for recent times, assuming n kids per couple and a lifespan of Y years, that's (n-2)/(2*Y)

This very simple model says that population growth will be exponential, with the rate of growth determined by lifespan and fertility rate. Population growth also looks kind of constant, naturally: (effective) fertility rate has not experienced order-of-magnitude level changes, and likewise for longevity. Plotting stuff on a log scale will tend to attenuate these minor changes and make salient the larger increases. See this example below:

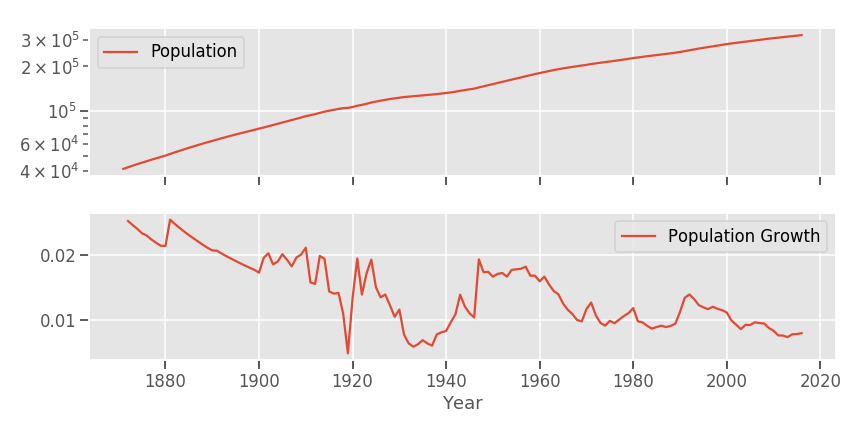
The smoothing power of exponentials

Even though population growth has fallen by a factor of two, the exponential seems to be look suspiciously like an straight line in the log plot and, if anything, it seems like growth has accelerated, not decelerated! GDPpc does look more like an stationary process, but still the point remains that exponential trends may not be as smooth as they seem. As an example, look at this:

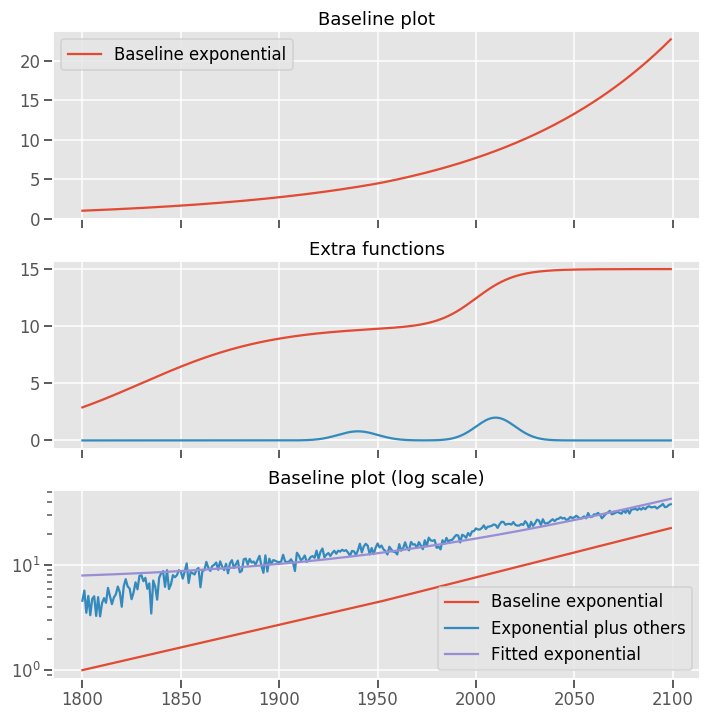
The red exponential is just an exponential. The "exponential plus others" is the same exponential plus noise,two sigmoids, two gaussians, and increasing its rate of growth by 10% in 1950. One can still fit an exponential to that one. And even though there is some clearly non exponential stuff going on inside of it, the exponential behaviour swamps everything else. One might then consider the puzzle of "Why is the blue line so smooth" and an answer would be: there's an exponential process driving it, plus other stuff that compared to it is inconsequential, so it is not that smooth to begin with.

Long run GDP modelling

So then, can we find a similar explanation for GDP? A model like the one for population.

One might first try to see if the phenomenon is local in time and space, and to some extent it is. GDP per capita growth was flat until 1700-1800.

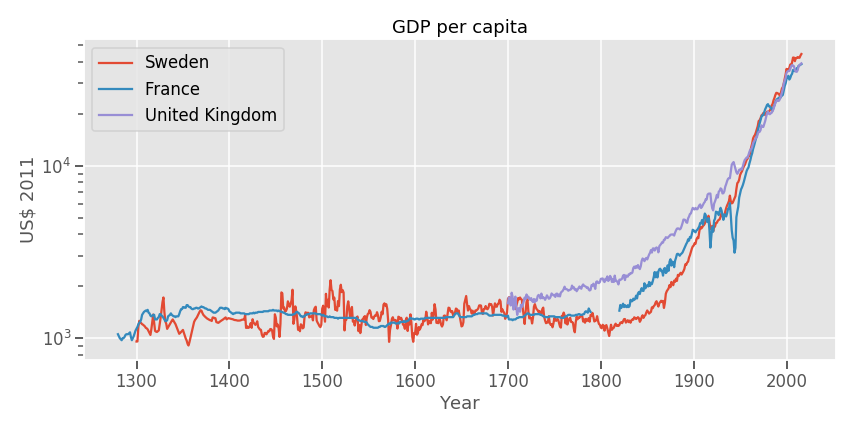
This was the Malthusian regime: GDP did increase, but as soon as it did, population increased to match it, keeping wealth per capita constant. Here we can also do a simple modeling exercise: GDP per capita will be that amount of wealth that allows a generation to, at least, reproduce itself. With a biologically-nudged setpoint for desired number of offspring above 2, we get population growth, and a constant quantity, GDP per capita. GDP is thus purely driven by population growth in this model, and our hyper-parameter, so to speak, is the desired number of offspring. (One can complicate this model to make it more realistic)

We can then ask: When did sustained growth began? That constant growth is the subject of this post. One usual answer is: During the Industrial Revolution. It may have been earlier, during the Scientific Revolution, but the fact remains that it happened then, and not during Roman times or during the Middle Ages. It is not the subject of this post to explain why, but insofar as the why forms part of the explanation of the constancy of growth, we can't help say something about it. Different authors put the why in different places: In an increase in status of the burgeois virtues (McCloskey), in the spread of an ideology of improvement (Howes), the rise of scientific thinking (Mokyr), or -breaking with the character of these explanations - a high ratio between wages and the cost of capital (Allen).

If we accept the first set of theories there are some questions that will be raised like "But the Greeks were inching towards science, why didn't growth began much earlier?" , but we can immediately go back on topic: What is there to science and a preoccupation with systematising that leads to constant growth?Here I won't say more than: Sharing ideas, building on top of other's, testing those ideas with experiments to discard wrong ones, finding out that nature has strict rules shifts one's focus between finding hacks and heuristics and looking more at generalisations and laws which have wider implications.

So, once we get to the Industrial Revolution and the Malthusian model breaks down, it is then when we begin to observe that constant rate of growth in GDP per capita. This occurs in different countries, in some earlier, in some later, and growth rates also tend to be faster in poorer countries, as they catch up with faster growing countries. With these caveats, we can say that for countries at the frontier, growth rates are similar, and have been for two centuries.

Long run per capita GDP modelling

The problem of constant GDP growth in general thus reduces to the problem of constant GDP per capita growth after the Industrial Revolution. Or it would if we assume that population and GDP per capita are independent. This seems true at first: Singapore and the US are both wealthy economies, but have vastly dissimilar populations. But we also know that in some tribes, when they decline in size, they forgot abilities and declines in wealth. A large population may also mean (The US is a good example) a linguistically, and institutionally homogeneous population, and that's good for trade, so more population, ceteris paribus, could mean more growth. In models of economic growth, a larger population also means more researchers, and in general more ideas being discovered and implemented. Thus, slowing population growth can also lead to slowing -GDP per capita- growth. However, ultimately in these models what drives growth is finding new ideas.

In growth economics, standard models of the economy usually decompose GDP in labor, capital and productivity, so Y=f(A,L,K). Here we need not concern ourselves with the form of the function f. We can look at L, labour, and note that man-hours supplied in the economy is populationfraction workinghours worked (man-hours), and that, having dealt with population we can just say that neither the fraction of society that works nor the hours worked have changed by an order of magnitude, and so it won't have caused massive changes from an exponential growth point of view.

For capital, it is more interesting: Unlike Soylent Green, capital is not made of people so it is decoupled from population, and it can be accumulated. We can say that capital in one year equal capital in the previous year less depreciation of existing capital, plus investment, which will be a fraction of income in the previous year (Here we believe in Say's Law, and assuming a closed economy, so savings rate=investment rate). This would seemingly let us get lots of growth by means of accumulating capital, but not quite. The issue is diminishing marginal returns. Assume a Minecraft economy with a bunch of people punching trees to collect wood. That gets you an amount of wood per year. Next, the technology of axe-making is introduced. Now some wood can be made into wood axes. This increases the amount of wood that is chopped every year, and the number of axes being used until one hits the labour constraint (there are only so many people that can wield the axes).  Even with an exponentially increasing population, the extra benefits of the axe is a one off thing. This illustrates that accumulating capital gets you some initial growth, and then no more. To get continued economic growth you need productivity growth, finding better ways of turning inputs into outputs.

Two cynical arguments

So, the initial question ends up becoming 'Why does productivity growth grow at a constant rate?' Does it, one may ask? Before continuing our discussion we may consider two cynical arguments:

One, that GDP growth in general is not well calculated (and if it were, it would be less smooth). Alexey Guzey made the argument here.But I don't find the argument plausible: It's not just the US GDP, it's GDP everywhere, calculated by many different people. There's World Bank GDP, Penn World Tables GDP, Maddison GDP,OECD GDP,and nationally calculated GDP, and they broadly agree. For inflation I remember a similar concern: May it be that governments just lie about inflation? But the MIT Billion Prices Project calculated over time their own independent measure of inflation and again it agreed.

Two, that perhaps something in the way GDP is calculated leads tautologically to the conclusion of exponential growth. Again, this seems unlikely if one goes to the definition. Nothing in the definition of GDP, especially real GDP as opposed to nominal implies exponential growth, and GDP has been observed to rise, stagnate, and decline.

Long run productivity growth modelling

Productivity growth in the US and the UK looks like this:

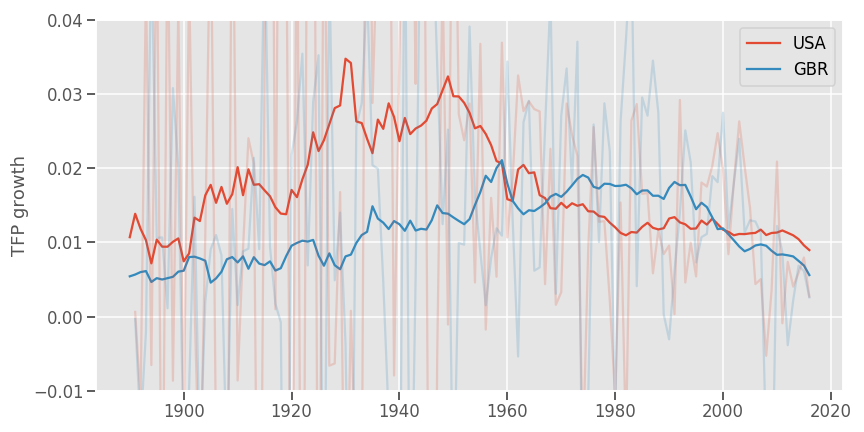
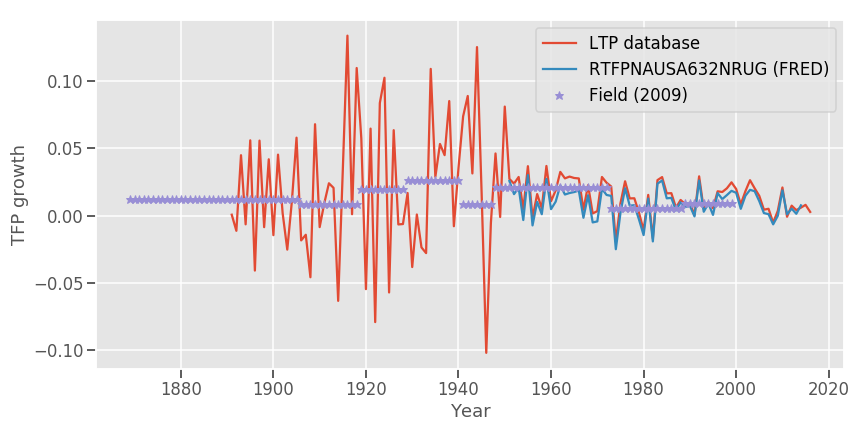
Just in case, (I've never used this dataset before), a comparison with FRED data and with Field (2009) for the US data.

One may instead be sceptical not of GDP but of how productivity is measured. Clark (2005) is an example of this argument,

The appearance of a sharp discontinuity in the rate of technological advance for European society around 1800 is very dependent on the weighting that is given to the various efficiency advances that were occurring before and after 1800.

The early economy did not lack technological advances, it was just that most of these were in goods that did not appear in the consumption bundle of the average consumer: imported spices, sugar, books, gunpowder, paints, silk textiles, glass, and paper. And there are many goods or services which were improved where we do not even have a price: clocks, music, theater, art, eyeglasses, and newspapers for example.

TFP measures, since they weight efficiency advances by the value of production in the economy as a whole, thus give very little weight to these advances. But from the perspective of consumers with tastes like ours we would not in any way find England 1200-1800 to be in technological stasis.

This still leaves several questions. The first is why real cost declines before 1800 tended to come overwhelmingly for goods consumed in quantity by a very small fraction of society? The second is whether the discussion above leads to a radical skepticism about ever defining the rate of technological advance in an economy? For there are all sorts of other weightings of goods in consumption that would produce very different patterns of efficiency advance over time.

Clark (2005)

However, we have already addressed that point: Indeed the right way to look at technology is to look at technology, not productivity. Measuring a value in a growth model is tricky, measuring the efficiency of an steam engine is simpler. Then, to look at productivity -this, and  not technology is what matters for growth- one can tie specific advances in technology to increases in productivity.

So: flat and then exponential, and then? GDP per capita could in theory continue to grow exponentially, but will it in practice? Growth models' answer is that as long as we keep producing new ideas that lead to productivity enhancements, growth will continue to be exponential, but after that, it will reach a steady state.

Long run idea growth modelling

Under the assumption of bounded useful (i.e. productivity enhancing) knowledge, useful knowledge would be like a mine. There would be a fixed amount, and exploiting some of it would initially leads to faster returns, but then over time, as the mine gets depleted, one has to work harder and harder to get more ideas out of it. If at the beginning you are not learning or you are not learning much, the initial growth rate is zero. As you knowledge grows, ideas beget new ideas and the growth rate increases. After this point, the growth rate could either continue increasing, stabilise, or decrease in the similar way as it went up. In the two first cases, growth will continue indefinitely, but because we have assumed bounded knowledge, it has to be the latter. This naturally then leads to sigmoid-like models.

An example of this is Huebner (2005)'s model, where he fits a modified gaussian to the rate of growth of 'significant innovation events' (There are around 8000 of those from his sources)

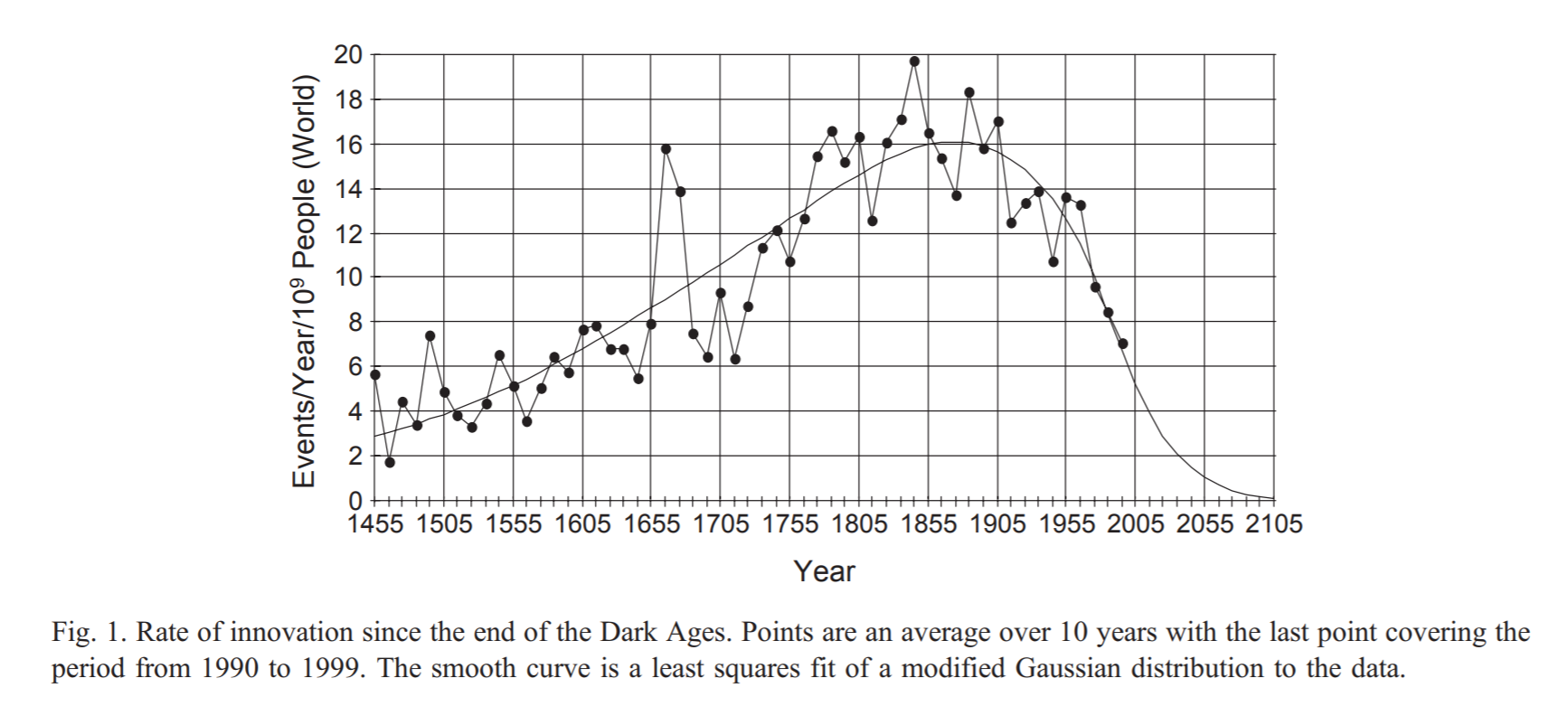
This model leads to an asymptote around 2100:

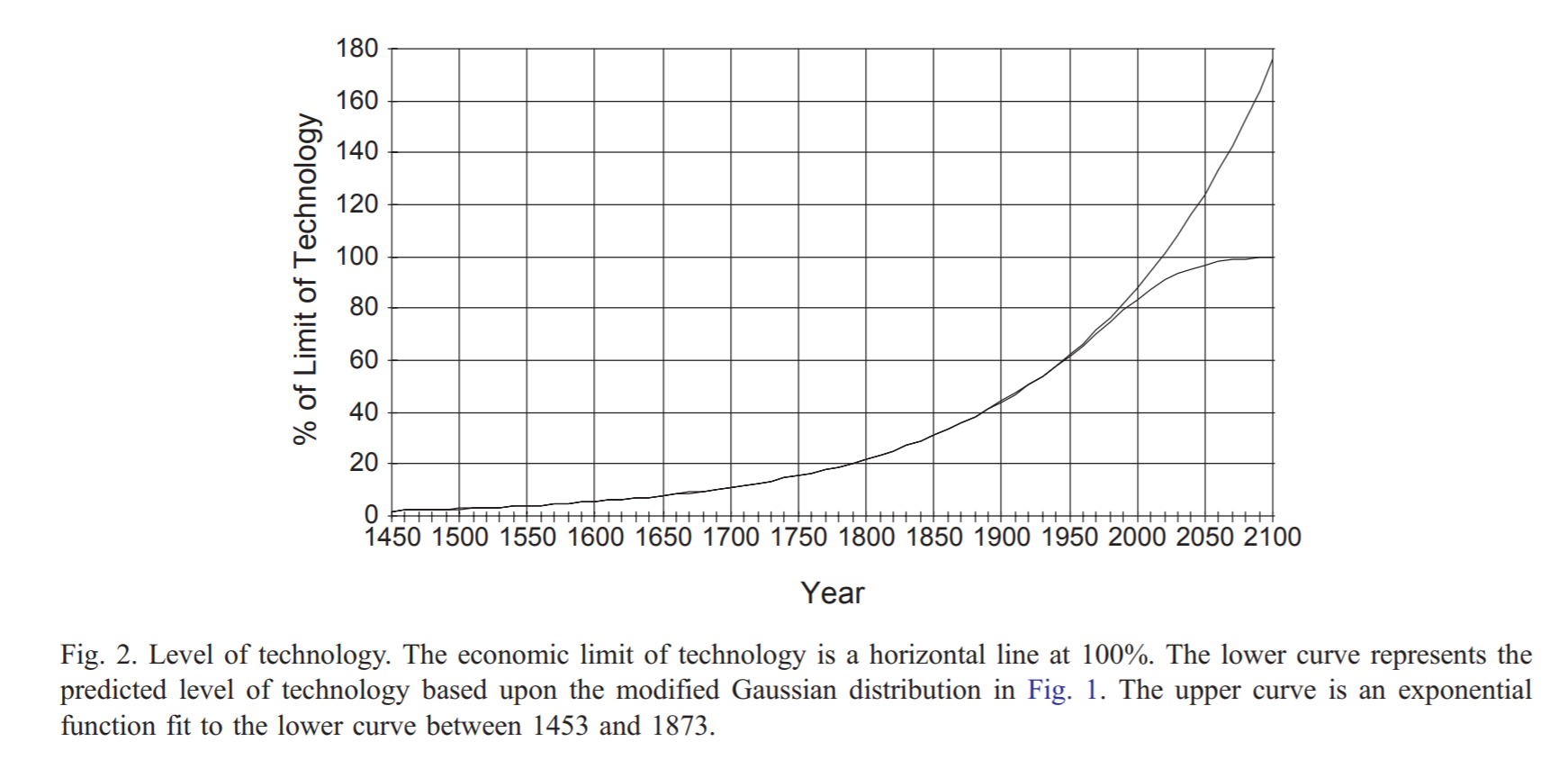
Interestingly, if we fit a logistic curve to the TFP data from the LTP database, we get this

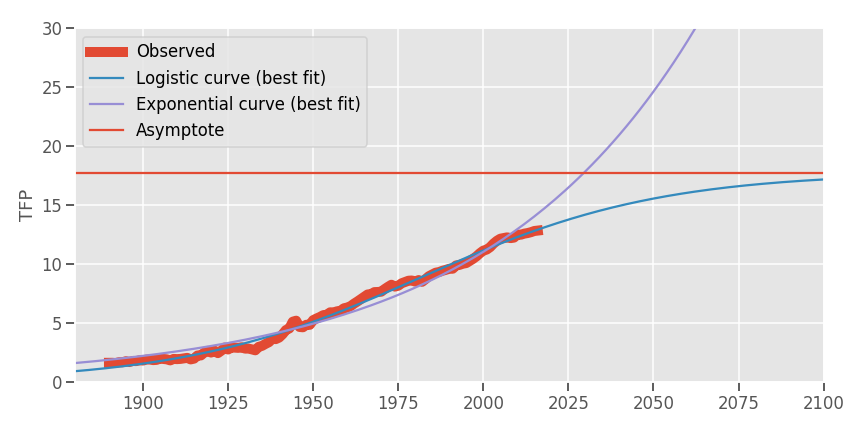
The problem of curve-fitting: Moore's law

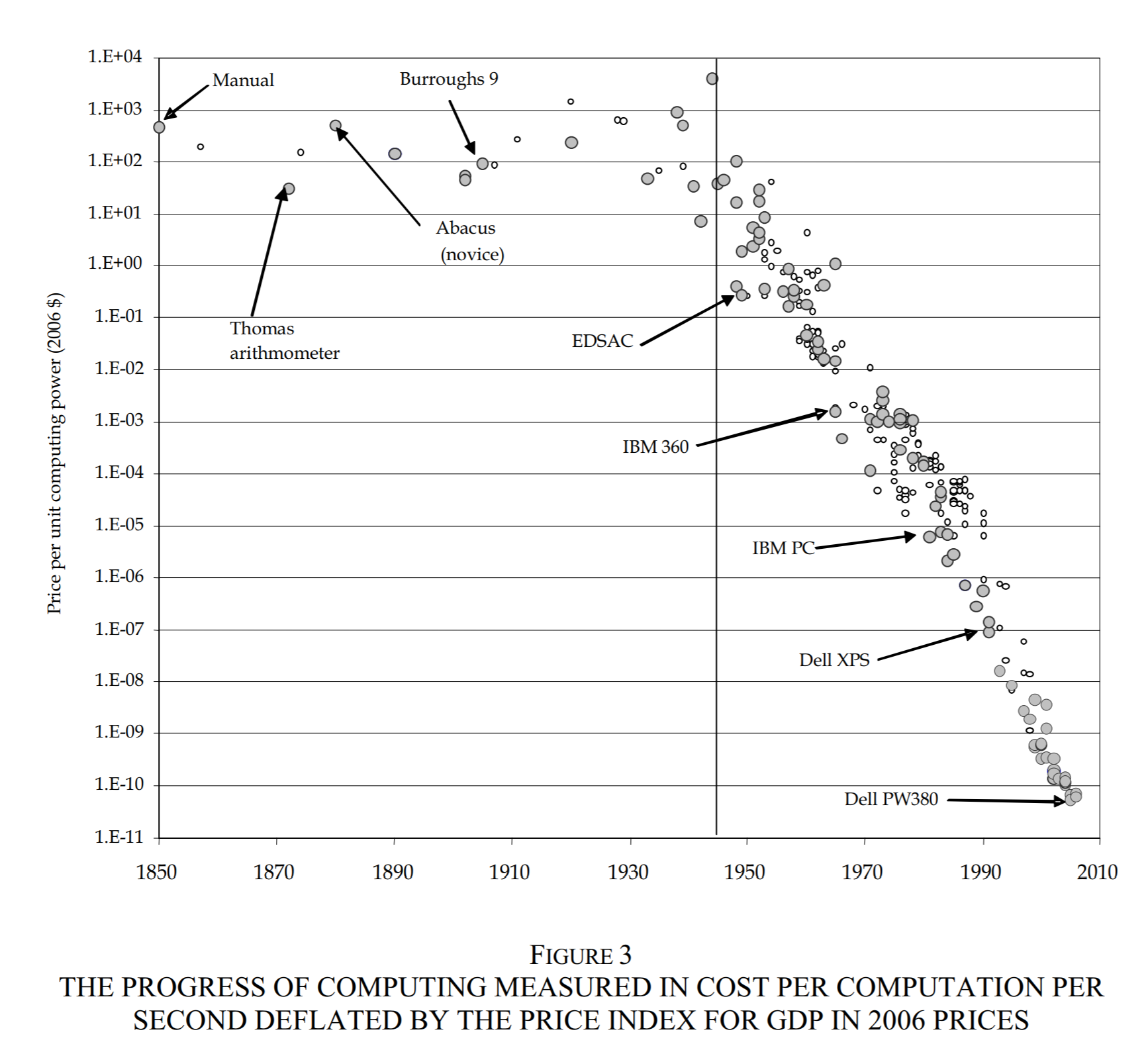
Once we have began fitting curves on things, it's hard to stop 🙃 . What about Moore's law? Most plots of Moore's law begin in 1970. But William Nordhaus (2005) tried to calculate an index of progress in computation by measuring how many computations were possible per dollar. I took this data from  Figure 3 below, inverted the axis, and took the logarithm.

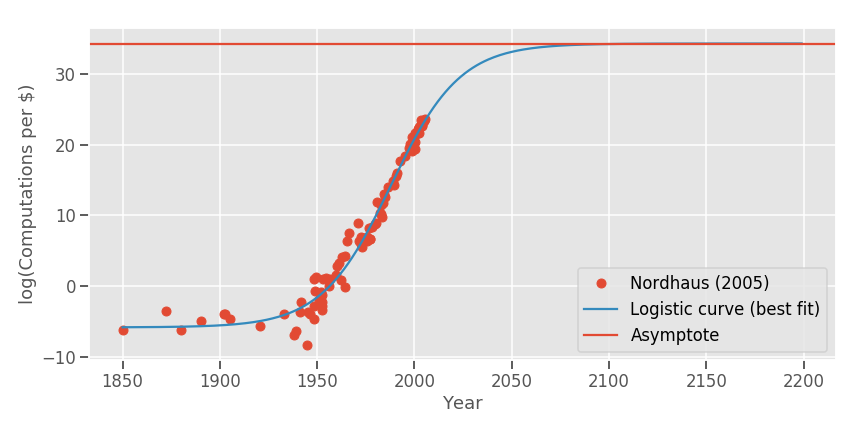
Not a bad fit! Oddly, papers that have tried to look at Moore's law in the past (Nagy et al., 2011) considered all sorts of fits but not a logistic fit. Do note that this is a logistic curve on a log, implying that the rate of growth may well be superexponential! But still, if the growth rate of a log(f(x)) is nil, the growth rate of f(x) will also be nil. That said, the model may not be that good: Let's suppose we are fitting the same curve with all the data available at year X, X<2005 .What would have happened is this:

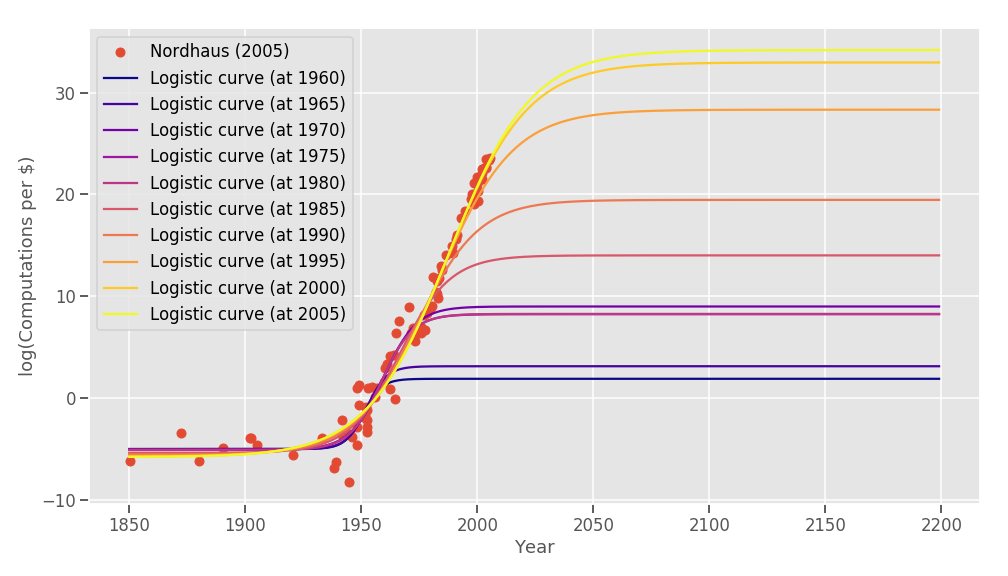
Doesn't look very good for the logistic model! (You may think, ah, but  the curves in recent years look closer together, it means the model is converging to the real solution! Not necessarily: It just means that there aren't that many new points in the last 5 year period. The point of this post is not to do a precise estimation, and a proper model won't be just a sigmoid anyway.

What is probably happening here is that is that if one takes a technology at any given point in time, and one assumes that current techniques will be used in the future, then one is constrained by the limitations of those techniques: One would be setting the amount of gold in the mine to be that allowed by current technology. But technology evolves. A similar phenomenon happened a few years ago in US oil production. The production curve of oil fields tend to also be logistic, thus the rate of extraction per year is broadly a a Hubbert's curve. People predicted an imminent Peak Oil, which would have catastrophic consequences, etc. But then shale oil happened:

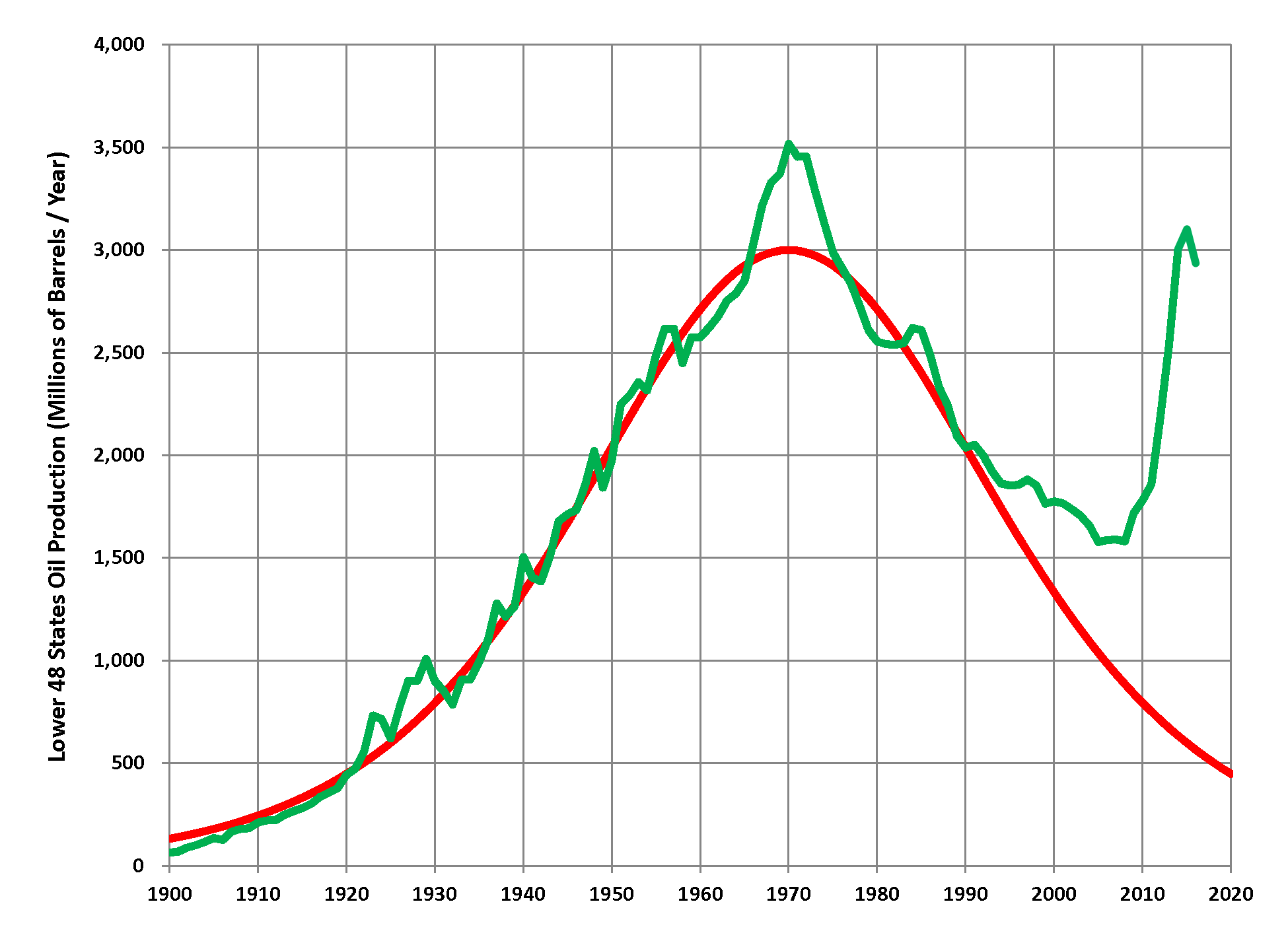
At the end of the day, however, the underlying prediction is still correct. If one takes away shale oil from the curve, ones still sees a decline. The why that peak suddenly appears out of nowhere is that a "new mine" opened up: the technology that allows for economically profitable fracking matured enough to be used and used it was. Thus, instead of modeling the rate of growth of TFP as one big Hubbert's curve (or similar), we could model it as a succesion of curves, each representing a new technology. Discovering a new technology is adding a new term to the model, a term that didn't make sense before.

Case study: aircraft speed

It's interesting to study this particular case because I'm an aerospace engineer /~~airplanes are cool / it's a commonly cited of technological slowdown / ~~ I wanted to scrape some data/ There must be a periodic post about airplanes in Nintil why not.

People commonly point to the fact that no commercial aircraft flies faster than Concorde, but that's an unfair comparison: Concorde was a politically driven project that would have not happened under natural market conditions. But indeed, the fastest aircraft now is basically as fast as the fastest aircraft decades ago, flying at around Mach 0.85.

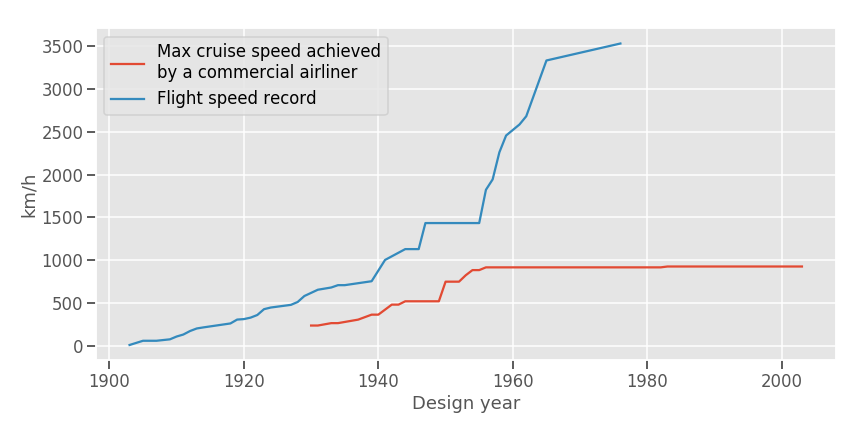
The cause for this is a nonlinearity: Mach 0.85 airspeed causes wind speeds of around Mach 1 in the wings (Aerodynamics 101: Wings work by, among other factors, creating a gradient of pressure. But what is less known is that doing that also induces different speeds: The air flows faster in the upper surface). At Mach 1 and slighly past it you get shockwaves and increases in drag, leading to poor performance. At faster speeds, however, drag goes down again (but not as low as in the subsonic regime). And then, the optimal geometry to fly supersonic is different than that for flying subsonic, and this makes it really hard to design aircraft that have to fly at both. (Also, supersonic flight was banned in the US). This is a case where "taking what works and tweaking it a bit" doesn't work anymore, you need a radical redesign, relative to other technologies. It is also a case where even when you can still continue with the trend  (The fastest non-prototype airplane, the SR-71 Blackbird achieved 3500 km/h back in 1976), economics will prevent you from doing so: What matter is that the aircraft can fly and pay for itself.

Commercial supersonic aircraft are not an impossibility, and progress has not stopped there: Boom Aerospace is developing a supersonic airliner capable of Mach 2.2 (Concorde cruised at Mach 2). Boom says the price of such a (return) ticket will be similar to today's business class (3-5k£) vs Concorde's roughly twice of that. Boeing is even toying with the possibility of a hypersonic (Mach 5) airliner but don't lose your sleep over that one yet. Likewise, there's Elon Musk idea of skipping the airplane altogether and shooting for rockets. This is to say, airplane speed improvements are not over yet for sure. A question would remain of why haven't speeds began improving already, and I would point to the very specific factors above, but then one could argue that it doesn't feel like a good enough explanation: It's taking the facts and saying 'Ah, it required a conceptual breakthrough/Well, you see,everything is smooth because it's just incremental improvements'. Ideally we should be able to predict when something is going to take time if we had a proper and pleasing explanation that applies for technology in general, but I leave that outside of the scope of this post.

Case study: Genetic sequencing

The cost of genetic sequencing has been falling dramatically in recent years. However, that rate has not been regular:

The rate of growth of the above curve can be modeled by the sum of two gaussians,

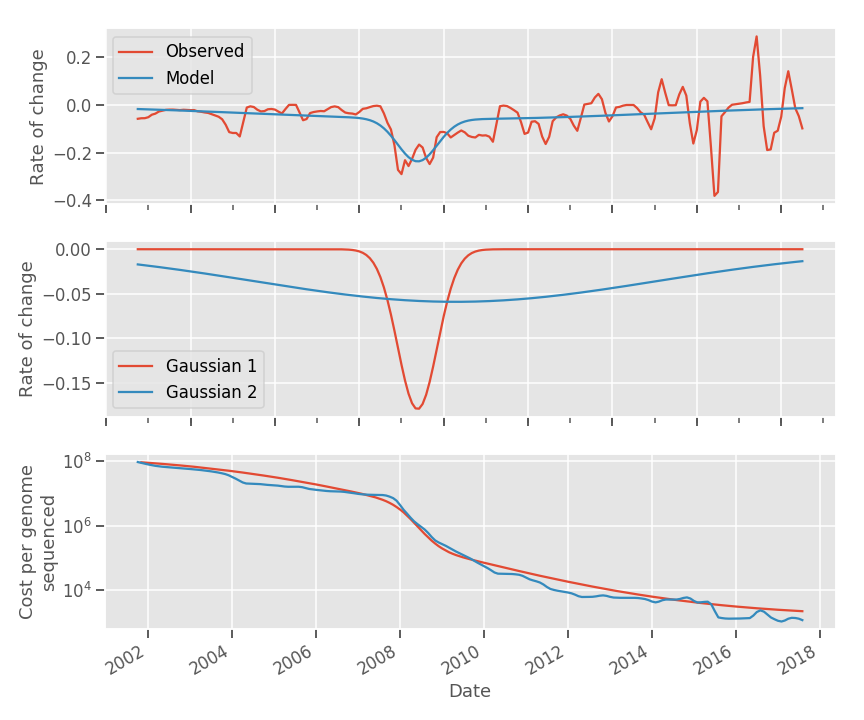
In 2007-2010 there was a sudden decrease and then the growth rate went back to where it was. Some point to the appearence of radically new ways of sequencing genome. The underlying trend may be the 'learning by doing' effect.

Case study: Light

The same approach can be followed for price of a unit of lighting (lumen-hour) if we take the data compiled by Max Roser here:

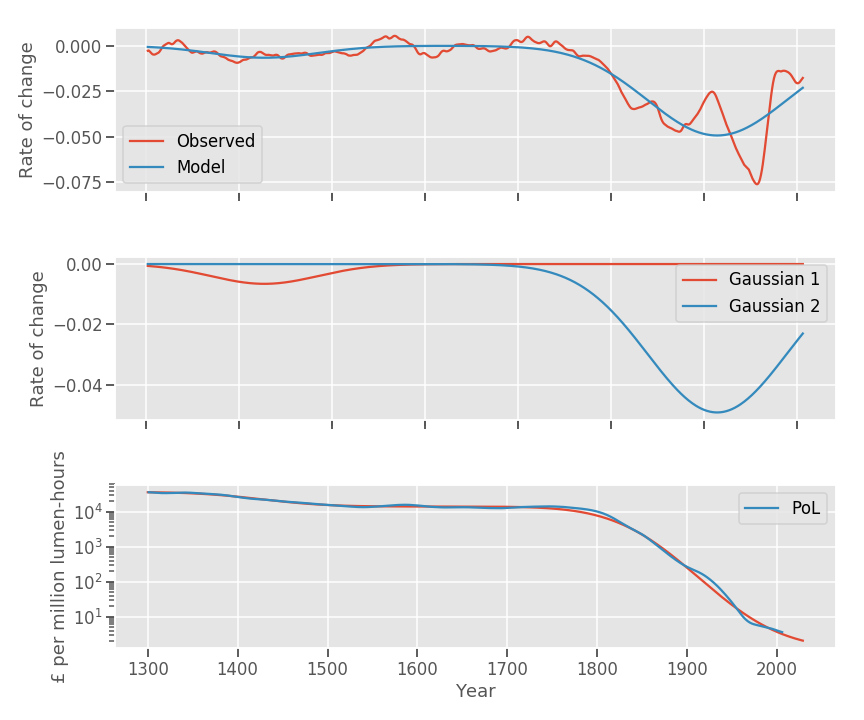
The general point here is that an increasing-and-decreasing slope of the rate of growth seems to model well the exploitation of a finite stock of resources (Note: I arbitrarily fitted two gaussians, but one should have one per technical 'paradigm' that gets exploited), but as we saw with the case of Moore's law, if the mine gets deeper, if we find a radically new way of generating light, or design processors , then we get another gaussian in the model, and the growth rate can continue to hover away from zero.

Then, the question would become: Can we predict the impact and timing of future technologies? Is there a process we can model that would serve as an input to the previous 'mining' mode?

This question is tricky: If we knew all there is to know about future innovations, then we would invent them straight away! If we knew nothing, then I would end this blogpost right here. What I think can be said is that once we have assumed something in the proximity of the 'mine' model,we also accept that growth rates change. If we sum over all the technologies there are, it's not odd if the resulting curve is smooth. But! Don't technologies come in clusters sometimes (innovation begets innovation)? Wouldn't that then lead to different growth rates over time? Yes it does: And if you look at the TFP growth charts, TFP growth has not been constant over time. If every single innovation occurred at the same point in time (say, we discover all there is to be discovered in 1800), then I'd say that historical growth rates would be predictable with a single gaussian. On the other hand, if every innovation happens at a completely random time then growth rates again would be predictable due to the summation of all those curves. In the middle, if innovations were somewhat  autocorrelated then we would observe very changing growth rates, together with periods of both abundance and scarcity of new ideas.

We can empirically rule out both extremes, and we are left out with a mixture of randomness and autocorrelation, giving rise to a sort of constant, but not quite, rate of growth in TFP, driving, as argued, growth in GDP per capita, and thus ultimately, GDP growth.

Conclusion

GDP growth in the US after 1800 is relatively smooth. This smoothness is due to

• The smoothness of population growth, due to...
  • The lack of major(order of magnitude) changes in fertility
  • The lack of major changes in longevity.
• The smoothness of GDP per capita growth, due to...
  • The smoothness of the growth of available labour, due to...
    • The lack of major changes in the fraction of the population that works
    • The lack of major changes in hours worked per person
  • The smoothness of capital accumulation, due to...
    • The lack of major changes in savings rate
    • The lack of major changes in depreciation rates
  • The smoothness of productivity growth, due to...
    • The way the stock of ideas grows, somewhere between
      • A fully smooth case where all ideas at discovered at once, or where idea occurrence is distributed randomly.
      • A highly autocorrelated case where growth happens at irregular points in time, at different rates.
      • ... yielding approximately regular, but not quite, TFP growth

This, and the conclusion, assumes a model of bounded useful knowledge. To me this seems obvious to assume. But this does not tell us anything at all about when will growth come to an end. I've made remarks about some properties of the distribution of ideas over time, and I've made some skeptical remarks about fitting curves to data in past and extrapolating into the far future. I am not saying anything about the stock of knowledge that is left to know and apply, nor I'm saying anything about the efficiency of the idea-generating, and idea-applying processes over time. It can well be the case that a lot of science is waste. and that more could be done to make those productivity gains happen earlier, rather than later.

Comments from WordPress

• deweaver 2018-11-24T20:28:48Z

  Fascinating subject. All businesses have a long-term usually sigmoidal type growth curve with a decay at the end. Somehow a sum of sigmoidal curves appears as an exponential is not obvious.

  It appears that economists seem to view TFP and A (ideas in the growth equations) a bit different than the physical scientists view the concept of innovation and ideas. These concepts only appear in the GDPpc numbers after raw ideas have passed through several serial stages. The first stage is technological feasibility then economic feasibility and marketing feasibility onto financing and now regulatory/permissions by multiple regulators, bureaucrats, activist groups and politically connected existing players in the markets being targeted. Being a series system of "implemented innovation", the slowest stage becomes the rate controlling stage. Even an infinite number of excellent raw ideas that are economically and technologically viable can be delayed, stopped or blocked by the FDA, EPA, NOAA, Sierra Club, etc.

  Another blog on Nuclear Power demonstrates how the cost-effectiveness of nuclear power can be killed in the US via the regulatory system. Both good ideas and "learning while doing" becomes almost impossible in a system where every activist/regulators/nut group has veto power creating a "tragedy of the anti-commons" situation.

  Back when reactors in the US were economical (the early 70's), I went to work for Bechtel with my shiny new Ph.D. in the Nuclear/Environmental division. With my knowledge-base, I came up with a new way to handle some rad-waste problems that would save 10 million dollars on each reactor they were building while improving safety and controllability. Upon taking this idea up the line, I was informed by the division leader than it would cost more than the savings to get it through the regulatory bureaucrats while creating a significant delay and ordered to forget it. I switch to the environmental side cleaning up air pollution where ideas could be and were implemented.

  As the number of possible "ideas" and "innovation" is expanding at an exponential rate with scientific knowledge with a less than 10 year doubling time and as new ideas are also created by combinations of existing ideas (often from different fields) which is growing at factorial types rates (faster than exponentials), ideas are not the rate-limiting step in economic growth.

  Financing by AI and VC capital limits the banks and the Federal Reserve as a rate controlling factors. Good ideas can get money.

  This leaves the regulatory system and bureaucrats as the rate controllers in all areas of the economy that require premsissions, which is the largest fraction of the economy outside of Silicon Valley. Note that Apple and the others that required real-world facilities bypassed the decade-long delays of building a 100,000 employee factory in California by going to other countries for manufacturing.

  Why the impact of the regulators and bureaucrats on economic growth is proportional to growth level per capita is unclear. The present rate-limiting step was not present in the early 1900s when the government was insignificant. There is no reason to expect regulatory limitation to be the same in all countries as can be seen in aquaculture, which is growing at near double digits in all countries outside the US ( < zero growth). The US has the largest extended economic zone (EEZ) in the world and no significant offshore aquaculture is allowed and we import 90% of our seafood consumption with half of that being aquaculture product from other countries (like salmon from Norway, Chile, etc.).

  Perhaps looking at the other half of the shift of resources from the old decaying sectors to the young innovative growing sectors may be productive. A business with 10 to 20% advantage over direct and indirect competitors wins, but that means 80 to 90% of some other business must decay and they will fight back. Video games won resources relative to ornamental fish that decreased.

  The amount of resources associated with this decay function of a sum of sigmoidal growth with decay curves over time can be proportional to the size of the overall economy and can result in an exponential function overall. If decay is modeled as a % of the existing size of industry/sector and the number of industry/sectors on a per capita decay curve (like steel is in developed countries) is economical dominant, we get and exponential increase as that decay resources shift to the innovative growth area.

• Rational Feed – deluks917 2018-11-20T15:51:14Z

  […] On The Constancy Of The Rate Of Gdp Growth by Artir – The GDP growth rate in developed economies has been shockingly constant over time. The author looks at GDP, population, labour force size, capital accumulation and innovation over time. Case studies include: Aircraft speed and Moore’s law. Lots of charts. […]

• whoisnnamdi 2018-12-08T05:35:41Z

  Came here from Marginal Revolution a few weeks back - great blog post and super interesting decompositions of various growth patterns.

  I do think there is a danger in this exercise of simply data mining - not an accusation just something to be careful of.

  In case you are interested, I recently wrote a post on the topic of compound growth more broadly, where I include some example of GDP growth but also discuss other phenomena and statistics. Feel free to take a look if this topic is still of interest: https://whoisnnamdi.com/you-dont-understand-compound-growth/

• Friday assorted links - Marginal REVOLUTION 2018-11-23T17:40:08Z

  […] 3. On the constancy of the rate of gdp growth. […]

• 2018. november 27. | Magyar Tudományos Akadémia Közgazdaság- és Regionális Tudományi Kutatóközpont Közgazdaság-tudományi Intézete 2018-11-27T10:54:21Z

  […] GDP növekedési ráta állandósága On the constancy of the rate of GDP growth Posted on Nov 19, 2018 – […]