Progress in semiconductors, or Moore's law is not dead yet

Moore's law is relentless - Jim Keller

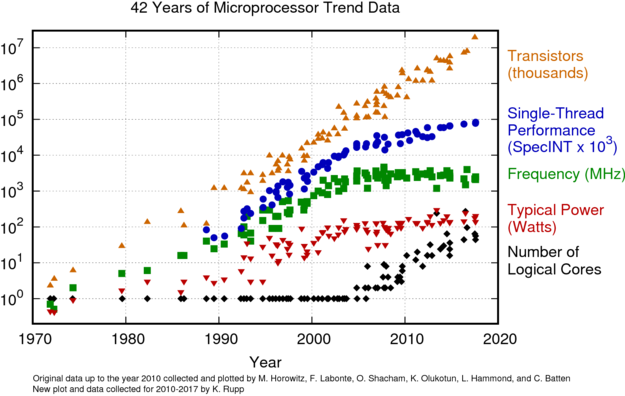
In its original formulation, Moore's law¹ was about cramming more transistors in ever decreasing surfaces; by that metric Moore's law continues unabated. However that's not the most interesting thing. As much of a feat of engineering it is, most people are interested in the end-product of the semiconductor world: performance.

Before moving onto that, here are some charts that show progress in the original Moore's law sense (ht Sam Zeloof for the data). Of note here is that progress has not been just on making transistors smaller (Even though there is a recent disconnect between the "marketing" node name and the real feature size; 7nm process doesn't mean necessarily 7 nm transistors). Interconnect layers refer to the multiple stacked layers that a chip has to route signals.

Performance

You may have noticed that we are getting processors with more and more cores; the latest from Intel (i9-10900K) or AMD (Threadripper 3900X) have 10 and 64 cores respectively. At the same time, frequencies don't seem to be increasing exponentially. The first computer I used ran at a few hundred MHz; years later, maybe around 2008 I recall getting a desktop with the first quad core processor that was released, the Q6600, which ran at 2.4 GHz. The latest i9 cores can go slightly below 5 GHz when all cores are active, and slightly above when it's only just one core. So in raw frequency during my lifetime as a computer user we have gotten a ~10x improvement. This sounds all nice and good, but when you look at recent times, it looks like getting above 5 GHz has been substantially harder than 1 GHz.

The argument made that adding more cores is not that impressive is that a lot of programs have not been designed to take advantage of this abundance of cores; and while now we could browse the web, watch videos, listen to music, and play games all at the same time, people don't tend to do this. If, say, your web browser tab only uses one thread then adding more cores is not going to make websites load instantaneously (And indeed the V8 javascript execution engine -which powers Node.js and Chrome- runs on a single thread; likewise Chrome's Blink rendering engine is single threaded; Mozilla is developing a multithreaded browser engine). Ultimately if there is just one task that cannot be parallelized, that will become the bottleneck for the application (Amdahl's Law). Thus, the argument identifies a more fair or accurate benchmark for measuring progress: Single threaded performance (STP), which is not affected by the number of cores; here it would seem like there is not that much progress, as STP is directly tied to frequency, and frequencies have not been increasing that much.

The argument about Amdahl's law is true; but its more naive form overlooks the fact that there can be progress in semiconductors even when frequencies are not increasing. For example, the CPU can fetch, decode, and execute multiple instructions per cycle (Pipelining, Superscalar processor), attempt to predict what's going to be executed next (Branch prediction), executing code before the CPU is sure it is needed (Speculative execution), introducing instructions to parallelize certain kinds of array operations (SIMD), or reorder the order of execution of the instructions. There is even a wikipedia entry for the Megahertz myth; trying to compare performance just by looking at frequency.

As a result, if we take the Pentium 4 540 (3.2 GHz), it achieves a performance of 153 in the Geekbench. In contrast, the i9-9900KS (5 GHz at full boost) gets a score of 1413, showing that it is possible to get 9.2x better (At least as measured by that benchmark) with just a 1.6x higher frequency. Multi-core performance of course shows greater improvement (44x faster).

There are other ways of making software go faster too; unsurprisingly writing better software can make it run faster; only that the ever increasing performance of CPUs lead software engineers to rely on Moore's law for speed, providing endless fodder for Jonathan Blow's endless collection of rants on the slowness of software.

However, and this is important, these kinds of improvements are one-off: Branch prediction cannot get better than 100%, or gains from SIMD eventually are offset from the parts of the code that cannot be vectorized.

Moore's law has been going on for a while; if one is willing to consider performance in an abstract sense that allows us to compare manual calculations with vacuum tube computers and integrated circuits we get this (From Nordhaus)

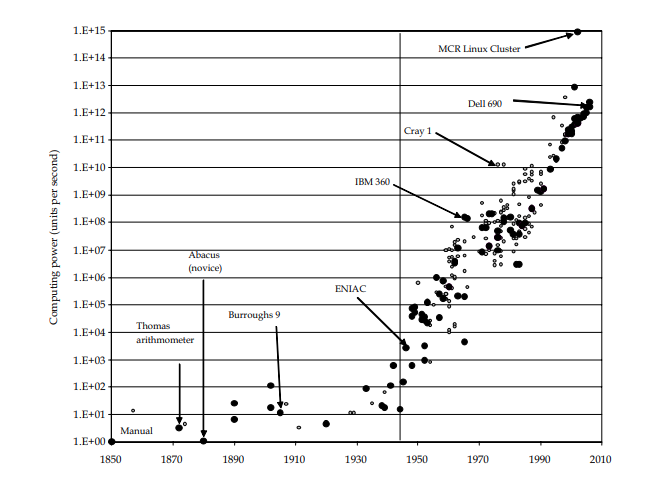
For reference, the first working transistor was built in 1947 in Bell labs; the first computer using transistors was built in 1954, and Moore stated what would later become "Moore's Law" in 1965.

As for the exact numbers, it's surprisingly hard to come up with updated benchmarks; but one I found from 2012 claims that while progress has halved recently, it keeps going at a rate of ~20% per year. If I do it myself (See the companion notebook in the github repo) using the SPEC2017 benchmark and take the fastest CPU in 2016 (Intel Xeon E5-2699A v4) and the fastest CPU in the benchmark (Intel Xeon Platinum 9282) the CAGR would be 27%. These are server-grade processors, so I did the same with Geekbench with the i7 and i9 ranges (Again see the repo) and I got ~9%.

Or one could also look at improvements in Apple's A cores. Looking at progress from the iPhone 5s to the iPhone 11 Pro max represents a ~31% annualized improvement. In the Android world (Looking at Samsung Galaxy S series, from the S6 to the S20 Ultra 5G) we similarly get a ~37% rate.

That may be the ballpark figure for the question "How much faster are CPUs getting", 9-30% every year, and this is half of what it used to be. Still exponentially improving, but not as fast. Moore's law in a broad sense is not dead (CPUs getting exponentially faster over time).

Making software fast

Here's a recent twitter thread that exemplifies how much faster can software get with the right design, no matter the programming language, maybe 2 or 3 order of magnitude (With just changing 2 characters in the code in one case). That may be a contrived and well studied example (Matrix multiplication in row vs column-wise ordering), but the general point is that understanding how the computer works can yield great benefits in performance. Another instance of this is, say, iterating over an array of numbers vs iterating over an array of structs that hold numbers and accessing them. Algorithmically, in the naive Computer Science sense, the complexity is the same; however performance can be wildly different. See here for a practical example of this.

But what about frequency, really

So I said that frequency is not getting all that much faster over time and that higher clock rates is a way to make CPUs faster, so why aren't we seeing much of an improvement there?. Or rather, why were we seeing an improvement during the past decade? Because of Dennard scaling.

Dennard scaling refers to increases in performance derived from shrinking the transistors. The idea here is that a smaller transistor can be operated at a higher frequency and at a lower voltage; ultimately for a given surface area power consumption stays the same, but you end up with more, and faster, transistors. So for a while manufacturers kept shrinking transistors and increasing frequencies (without reducing voltage) until around 2006 when a point was reached that it was hard to effectively dissipate the resulting power densities, which stopped Intel from pushing forward with their Tejas and Jayhawk architectures. The obvious question is why not just drop voltages? This is what is known as undervolting in the overclocking world, but the problem is that for a given frequency there is a minimum voltage required for the transistor to operate, go lower than that and transistors are not able to switch at the required speed, ultimately causing system crashes.

Power dissipation, power consumption in CPUs, for a given design, increases with the cube of frequency² At some point you end up with power densities rivalling those of a nuclear reactor and dissipating all that heat becomes incredibly complicated. Even using liquid nitrogen to cool processors, one can only go up ~9 GHz, and fitting phones or laptops with such system seems hard.

There is another reason, besides power dissipation, why frequency has not been increasing: wire delay. Inside the CPU, the time it takes for a transistor to signal its state to the next transistor is nonzero; so with a sufficiently large chain of transistors the time it takes for the signals to propagate can exceed the actual clock time; this puts a limit on the frequency of the entire CPU: It cannot be higher than the time it takes for a signal to travel the longest path in the chip.

A third, less important reason is that even if one manages to increase frequency to absurd levels, one is not going to see all that immediately being translated into more performance: Frequency of DRAM would also have to increase; and right now it is lagging behind that of CPUs. As one example,if the CPU wants to get something from main memory, by the time the item is fetched and sent the CPU may have completed hundreds of cycles. Hopefully it will have been doing something else with that time (speculating about branches of code that will possibly be taken), but it won't be as fast had it had instant access to the data, which is why CPUs have caches.

According to Hennessy & Patterson heat dissipation followed by wire delay are the two main issues that CPU architects are facing these days in order to extract more performance:

Today, energy is the biggest challenge facing the computer designer for nearly every class of computer. First, power must be brought in and distributed around the chip, and modern microprocessors use hundreds of pins and multiple interconnect layers just for power and ground. Second, power is dissipated as heat and must be removed. [...] Given that this heat must be dissipated from a chip that is about 1.5 cm on a side, we are near the limit of what can be cooled by air, and this is where we have been stuck for nearly a decade

[...]

In general, however, wire delay scales poorly compared to transistor performance, creating additional challenges for the designer. In addition to the power dissipation limit, wire delay has become a major design obstacle for large integrated circuits and is often more critical than transistor switching delay. Larger and larger fractions of the clock cycle have been consumed by the propagation delay of signals on wires, but power now plays an even greater role than wire delay.

What's next

More cores. Don't expect core count to stall anytime soon. AMD just released a 64 core chip. I wouldn't be surprised if by 2030 we have 128 core general purpose chips. However, remember that this only helps for problems that can be parallelised. This is good news for scientific computing and video/image rendering, but for day to day usage, it's not that relevant.

Besides more cores, there are a few things in the pipeline that Jim Keller discusses here to try to keep shrinking features (Enabling more performance). On other end maybe the solution is different instruction sets. Modern chips either run on x86-64 or ARM. But there are some emerging alternatives like RISC-V that may make it possible to get extra performance in the future, who knows. ARM - most processors on mobile devices are ARM-based - has also been making great improvements, as evidenced by the rate of progress of the processors found in mobile phones, greater than that of desktops.

If you want an all-things considered view, this is it: