One of the Collison questions is

Is Bloom's "Two Sigma" phenomenon real? If so, what do we do about it?

Educational psychologist Benjamin Bloom found that one-on-one tutoring using mastery learning led to a two sigma(!) improvement in student performance. The results were replicated. He asks in his paper that identified the "2 Sigma Problem": how do we achieve these results in conditions more practical (i.e., more scalable) than one-to-one tutoring?

In a related vein, this large-scale meta-analysis shows large (>0.5 Cohen's d) effects from direct instruction using mastery learning. "Yet, despite the very large body of research supporting its effectiveness, DI has not been widely embraced or implemented."

---

Answering the question requires first to explain what Direct Instruction and Mastery Learning mean.

Scope of the present article

This article is concerned with a general study of Bloom's two sigma problem, which in turn involves an examination of an educational method, mastery learning, and tutoring. I have also included a review of software-based tutoring. Later on I look at educational research in general, spaced repetition, and deliberate practice, as these seem closely related to the core topics of this review for reasons that will be obvious after reading through it.

I am only concerned here with student performance in tests, not with other putative benefits from education; I don't look in detail at what keeps students motivated, what makes them feel well, what makes them more creative, or better citizens.. I could have looked at longer term measures of success (e.g. income later on in life) but I couldn't find such studies.

As a general note, when discussing effect sizes here, unless otherwise noted, the effect sizes are of the intervention being discussed vs business as usual, using whatever educational method the school was using.

Definitions

The Two Sigma problem

Benjamin Bloom, decades ago, found that individual tutoring raised student's performance relative to a baseline class by two standard deviations, which is a MASSIVE¹ effect. As 1:1 tutoring is very expensive, he wondered if there are approaches that approximate such an effect that were applicable for larger classrooms. Finding such a method was the "two sigma problem". And Mastery Learning seemed to be the promising way to solve it.

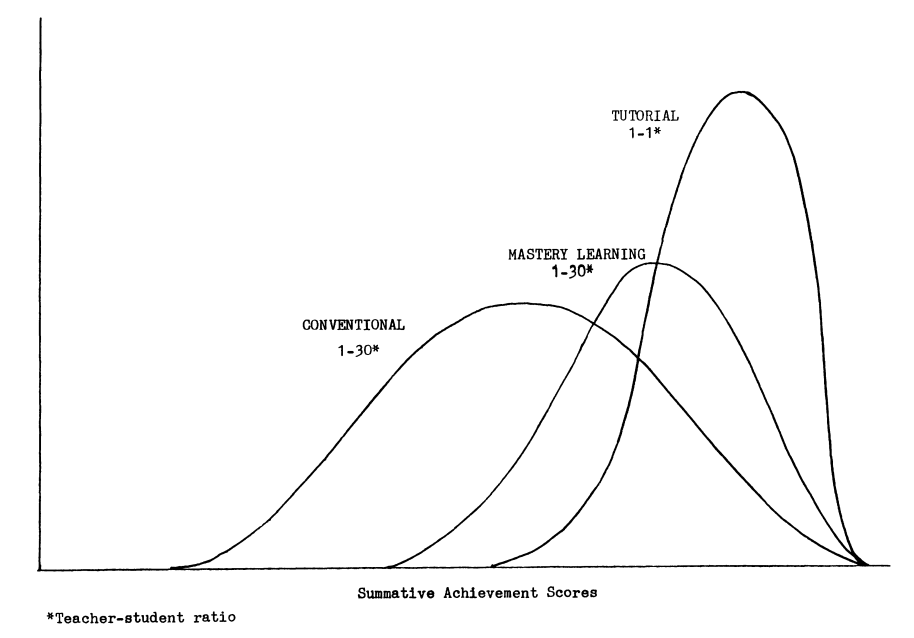
Direct Instruction

From the meta-analysis cited above, Direct Instruction is a teaching program originally developed by Siegfried Engelmann in the 60s that assumes that any student can learn any given piece of material, and this will happen when

(a) they have mastered prerequisite knowledge and skills and (b) the instruction is unambiguous.

This doesn't sound that helpful; fortunately the National Institute for Direct Instruction has a bit more information.

There are four main features of DI that ensure students learn faster and more efficiently than any other program or technique available:

Students are placed in instruction at their skill level. When students begin the program, each student is tested to find out which skills they have already mastered and which ones they need to work on. From this, students are grouped together with other students needing to work on the same skills. These groups are organized by the level of the program that is appropriate for students, rather than the grade level the students are in.

The program’s structure is designed to ensure mastery of the content. The program is organized so that skills are introduced gradually, giving children a chance to learn those skills and apply them before being required to learn another new set of skills. Only 10% of each lesson is new material. The remaining 90% of each lesson’s content is review and application of skills students have already learned but need practice with in order to master. Skills and concepts are taught in isolation and then integrated with other skills into more sophisticated, higher-level applications. All details of instruction are controlled to minimize the chance of students' misinterpreting the information being taught and to maximize the reinforcing effect of instruction.

Instruction is modified to accommodate each student’s rate of learning. A particularly wonderful part about DI is that students are retaught or accelerated at the rate at which they learn. If they need more practice with a specific skill, teachers can provide the additional instruction within the program to ensure students master the skill. Conversely, if a student is easily acquiring the new skills and needs to advance to the next level, students can be moved to a new placement so that they may continue adding to the skills they already possess.

Programs are field tested and revised before publication. DI programs are very unique in the way they are written and revised before publication. All DI programs are field tested with real students and revised based on those tests before they are ever published. This means that the program your student is receiving has already been proven to work.

Direct Instruction is highly scripted, including even the words they should speak while teaching.

Note that Direct Instruction (titlecase) is not the same as direct instruction (lowercase), there are various programmes around that have "direct instruction" in the name, like Explicit Direct Instruction . Unless otherwise noted, we'll be talking about Direct Instruction in this review. Both are teacher-centered methods in that the teacher is seen as the one who is transmitting knowledge to the student rather than, say, the student being aided by the teacher in a quest to discover knowledge. Direct Instruction is regulated by the National Institute for Direct Instruction, as mentioned above, while direct instruction is not.

Mastery learning

Mastery learning (ML) is not the same as Direct Instruction, but ML is a component of Direct Instruction. It is also one of the methods Bloom originally looked at, so we also examine ML in this review. One key difference is that ML does not called for scripted lessons, while DI requires them.

The key principle of ML is simply to force students to master a lesson before moving on to the next one. At the end of each lesson, on a monthly or weekly basis, students' knowledge is tested. Those students that do not pass are given remediation classes, and they have to re-sit the test until they master it. This can be done in a group setting, as with Bloom's original Learning for Mastery (LFM) programme, or individually, as in Keller's Personalized System of Instruction (PSI), where each student advances as their own pace.

Summary

• The literatures examined here are full of small sample, non-randomized trials, and highly heterogeneous results.
• Tutoring in general, most likely, does not reach the 2-sigma level that Bloom suggested. Likewise, it's unlikely that mastery learning provides a 1-sigma improvement.
  • But high quality tutors, and high quality software are likely able to reach a 2-sigma improvement and beyond.
• All the methods (mastery learning, direct instruction, tutoring, software tutoring, deliberate practice, and spaced repetition) studied in this essay are found to work to various degrees, outlined below.
• This essay covers many kinds of subjects being taught, and likewise many groups (special education vs regular schools, college vs K-12). The effect sizes reported here are averages that serve as general guidance.
• The methods studied tend to be more effective for lower skilled students relative to the rest.
• The methods studied work at all levels of education, with the exception of direct instruction: There is no evidence to judge its effectiveness at the college level.
• The methods work substantially better when clear objectives and facts to be learned are set. There is little evidence of learning transfer: Practicing or studying X subject does not improve much performance outside of X.
• There is some suggestive evidence that the underlying reasons these methods work are increased and repeated exposure to the material, the testing effect, and fine-grained feedback on performance in the case of tutoring.
• Long term studies tend to find evidence of a fade-out effect, effect sizes decrease over time. This is likely due to the skills being learned not being practiced.

Effect sizes

Assessing if an effect size is meaningful may be hard. A common way of doing so is as follows:

Effect size	d
Very small	0.01
Small	0.20
Medium	0.50
Large	0.80
Very large	1.20
Huge	2.0

However, one should be able to finetune the descriptive language used, by using a domain-specific reference. In this case, the average effect on performance from one year of schooling (going from 5th to 6th grade) is d=0.26 for reading performance, and the average effect from 141 large scale RCTs of educational interventions is 0.06, from Hugues & Matthew (2019). Because of this, I will be using a scale adapted from Kraft (2018):

Effect size (E.S.)	d
Small	<0.05
Medium	0.05-0.2
Large	0.2-0.5
Very large	0.5-1
Extremely large	1-1.5
Huge	>1.5

With that in mind, here is the summary of the main results, along with the best studies I could find to back up the claims. For comparison, I include Bloom's findings:

Method	E.S. (general)	E.S. (disadvantaged)	E.S. (Bloom)	Key references
Tutoring*	Very large	-	Huge	VanLehn (2011)
Software-based tutoring (High quality)*	Very large	-	-	VanLehn (2011), Kulik & Fletcher (2016)
Mastery learning**	Medium	Large	Extremely large	Kulik et al. (1990), Slavin (1987)
Direct Instruction**	Medium	Large	-	Borman et al. (2003), Stockard et al. (2018)

* With really good tutors and really good software, the effect size can indeed be Huge.

** When considering narrow knowledge of a series of facts, or basic skills taught at the elementary level, the effects of ML and DI can be Large for the general population and Extremely Large for disadvantaged students.

The evidence behind direct instruction

The meta-analysis I start the article with has a literature review, noting that all the previous literature, systematic reviews, and meta-analyses do show strong, positive effects of DI. This is no "mixed results" literature, which by itself is quite surprising, even suspicious; it is rarely the case that I find something so good and apparently uncontroversial.

DI/ML is what, as the meme goes, peak education looks like; you might not like it but it's the truth (as far as test scores are concerned).

In the late 1960s, DI was accepted as one of the programs to be part of Project Follow Through, a very large government-funded study that compared the outcomes of over 20 different educational interventions in high-poverty communities over a multiyear period. Communities throughout the nation selected programs to be implemented in their schools, and DI was chosen by 19 different sites, encompassing a broad range of demographic and geographic characteristics. External evaluators gathered and analyzed outcome data using a variety of comparison groups and analysis techniques. The final results indicated that DI was the only intervention that had significantly positive impacts on all of the outcome measures (Adams, 1996; Barbash, 2012; Bereiter & Kurland, 1996; Engelmann 2007; Engelmann, Becker, Carnine, & Gersten, 1988; Kennedy, 1978). The developers of DI had hoped that the conclusions of the Project Follow Through evaluators would lead to widespread adoption of the programs, but a variety of political machinations seem to have resulted in the findings being known to only a few scholars and policy makers (Grossen, 1996; Watkins, 1996).

Some of those interventions are (And I hadn't heard of them before): Direct Instruction, Parent Education, Behaviour analysis, Southwest Labs, Bank Street, Responsive Education, TEEM, Cognitive Curriculum, and Open Education.

Most of these actually caused a substantially lower performance compared to traditional school instruction. This supports the idea that at least on the metrics measured by Follow Through, the choice of educational methodology matters. In particular, the worst performer, Open Education sounds like something hip teachers would find cool:

focused on building the child’s responsibility for his own learning. Reading and writing are not taught directly, but through stimulating the desire to communicate. Flexible schedules, child-directed choices, and a focus on intense personal involvement characterize this model.

The effect sizes found in the meta-analysis are around 0.5, which, in the social sciences are considered to be fairly high.

The paper also looks at variability of the results between studies. Because methodology differs, it could be that the estimate is overstated because of the overabundance of shoddy studies. But even when controlling for everything you might think you can control for, the effects still remain, or so they claim; and the control variables did little to reduce it: It seems a very robust effect that shows up no matter how you slice the data.

As far as meta-analysis go, this is good, perhaps too good. I am reminded of Daryl Bem's now infamous meta-analysis on the possibility of some people being able to see the future. If the underlying literature is not good then the meta-analysis will yield biased estimates.

Critiques of DI

Sounding suspiciously good, I tried explicitly searching for criticism of DI.

One broad critique, more of a warning is that a substantial part of the literature on DI has been produced by people associated with the National Institute for Direct Instruction (NIDI), including the meta-analysis with which this article begins; that said the meta-analysis itself found no difference between the NIDI-sponsored studies and other studies.

Here's one professor of education, saying that sure, DI works at what it's designed to do, but, he argues, the price is an environment devoid of creativity, joy, and spontaneity. He does not give evidence for this, nor were these tested in the meta-analysis from before.

Alfie Kohn, an education researcher has an essay up with a critique of DI, starting with the Follow Through study. He also mentions that DI techniques have led, in some cases he cites, to students knowing well the material but being incapable of a deeper understanding or generalization.

Eppley & Dudley-Marling (2018) find the DI literature wanting. They look at work published between 2002 and 2013 and find that the literature is low quality, claiming that it doesn't work at all, except in a very limited number of cases, with a small effect. But they don't seem to quantify this, it's not a meta-analysis, nor do they comment on previous systematic reviews and meta-analysis that do find positive effects.

The What Works Clearinghouse reviewed 7 studies of Direct Instruction, out of which only one was considered good enough to include in their summary of evidence. They concluded that it has no effect. The study in question was an RCT with 164 students with learning disabilities and very low IQ (mean 76) at a pre-school level (mean age ~5).

As one might imagine, the NIDI people have a page dedicated to answer the above. Now, given that the WWC didn't review that many studies, and the study they did look at was a very atypical sample, I'm going to ignore this and look at more studies.

I have to mention that one of the authors of the meta-analysis co-authored a paper (Stockton & Wood, (2016)) where they question that priority should be given to RCTs when assessing the quality of the evidence.

On the other hand, the anti-DI camp also has their share of bad arguments.

The quality of the Direct Instruction meta-analysis

Table 1 in the meta-analysis, discussing effect sizes (average is ~0.5) have tight confidence intervals around that value. But then, when we get to table 3 discussing the effects of study designs on the effect sizes, we see that the effect of a study being randomised is quite negative, and so is adjusting for initial scores or IQ. Sample size itself didn't have much of an effect.

Let's try to look at the best studies, and see what we find. They mention that there is an appendix with the specific studies they looked at, but I couldn't access it.

Paper	Sample size	Focus	Effect size
Stockard et al. (2018)	328 (studies)	Meta-analysis being discussed (For reference)	~0.5
Flynn et al. (2012)	64	Foster children, 6-12 y.o. Using individual tutoring. RCT. Using (d)irect (i)nstruction.	Reading: .29, Spelling: -.08, Simple Math: 0.46
Cobern et al. (2010)	180	8th grade students, comparing DI vs "inquiry-based teaching " (IBL) RCT Using (d)irect (i)nstruction.	Science: 0.12 (vs IBL, not significant)
Harper (2012)	91	Foster children,educationally disadvantaged. 6-13 y.o. Using small group (4 students) tutoring. RCT Using (d)irect (i)nstruction.	Reading: .4, Spelling: .25, Simple Math: .34
Borman et al. (2003)	48 (studies)	Meta-analysis, educationally disadvantage kids	.15~.25 (In the top 3 of 29 learning models evaluated)2
Stockard (2015)	19 (studies)	Review of NIDI studies published after Borman's review. Non-RCTs are included.	-1.1~1.13 , average .35
Slavin (2011)	1 RCT, 3 matched studies	Best-evidence synthesis of various methods.	.25 for the RCT up to 1.18 in matched studies. In all cases, disadvantaged students, in the 1.18 case, mentally retarded students. The RCT is an unpublished PhD thesis.

I am sampling a few, but not cherry-picking: A pattern emerges: most DI studies are done on underprivileged students. It can be, and indeed, it is, the case, as we'll see later with mastery learning, that educational methods have more of an impact on those lower skilled kids. In the Stockard meta-analysis there is a reference to a 1999 review focusing on general education, rather than disadvantaged students, but they cite no specific papers beyond a 1996 book from Adams and Engelmann (1996), the originators of DI. The average effect they found was .87, not being much different between regular education and special education, and the effects were larger (Above 1 sigma) for adults.

But then, given that this effect is twice as large as the one found in the later meta-analyses makes you wonder about the quality of the literature. After reviewing the literature, there does seem to be some evidence that there is an effect from DI on kids with low skills, this effect being probably not larger than 0.4. For regular kids, we don't have much to work with. This may be one of the reasons why DI has not been more widely adopted in general.

The evidence for mastery learning

The most well known large-scale implementation of mastery learning is Khan Academy. There was an RCT ongoing, showing no meaningful effects.

Best Evidence Encyclopedia, maintained by Robert Slavin, a website collecting evidence on what works in education, did a review on diverse methods for teaching Maths, finding no effect in middle/high school, and limited evidence of a larger effect for elementary school. (They only included five studies, with effect sizes ranging from -0.18 to 1.08)).

This may sound surprising in light of the above. But a likely explanation is that all these studies are not using the exact same methodology. With Direct Instruction, we have an Institute regulating what DI is and how exactly it has to be done. With mastery learning, it's unclear exactly what counts and what doesn't.

The meta-analytic literature on mastery learning goes back to 1983, the last study of that period, Kulik et al. (1990) found large effect sizes for less able students (d=0.61) and medium sized for more able students (d=0.4), noting also that the difference between these two groups is not statistically significant in their sample. This meta-analysis covers programmes ranging from a few weeks to a few months, K-12 education, and college, and all kinds of subjects and mastery levels (Some variants of ML asked for perfection, others were okay with 80% on tests to advance to the next unit). As in Bloom's study, more demanding mastery learning methods yielded better results, with the most difference seemingly being between the 81-90 and the 91-100 studies. In other words, increasing the requirement from, say 70% to 80% doesn't do much, but increasing it to 90% or 100% (perfection) does. Importantly, the outcome varied substantially depending on how students were tested, a topic we'll return to in the next sections. When considering only standardised tests, not designed by the teachers or experimenters themselves, the effect size is tiny (0.08), while those that used experimenter/teacher made tests got a more impressive 0.5. When just the mastery learning programme that Bloom designed (Learning For Mastery,LFM) is included, the effect size rises to 0.59.

Cook et al. (2013) studied mastery learning as applied to medical education, covering 82 studies, finding an large improvement in skills (ES=1.29), and moderately large ones for patient outcomes (ES=0.73). Findings were highly heterogeneous, and so the authors caution that they have to be interpreted on a case by case basis. If this were true, it would be great news for healthcare!

In the most common general assessment of mastery learning, by Guskey (2015) is also favourable to it. There is one exception to the generally favourable systematic reviews and meta-analyses, Slavin (1987) who picked a subset of the literature he deemed to be of higher quality, finding almost zero effects. Later studies kept finding positive effects; Guskey refers readers³ to Kulik et al. (1990) as for why many thought Slavin's review was not a good one. It's useful to stop here to explain what Slavin's critique was and what the replies were, and I'll do that in the next section. I'll just finish reviewing other meta-analyses first.

Summaedu.org compiles other meta-analyses. Oddly, an earlier meta-analysis also by Kulik (1983) found a small effect size (0.05), similar to what Slavin would find later in his 1987 paper. The earlier meta-analysis covers grade 6 through 12, and the authors say that for college students they still believe effects are large. Even then, the 1990 and 1987 metas are not covering the same literature, not even for K-12 education (remember, the 1990 meta aims to cover all levels) if you look at the studies covered. The 1987 paper aims to cover all kinds of mastery learning implementations, the 1990 focuses on two (Personalized System of Instruction, and Learning For Mastery). To make things more puzzling, there is one more meta-analysis from Kulik (1987) that again says mastery learning works also for pre-college education. Wtf!

So what's up with the 1983 paper?

Paper	Studies	Focus	Effect size	Systems covered
Bangert-Drowns, Kulik & Kulik (1983)	51	Secondary school	0.05	IPI, PLAN, PSI
Kulik, Kulik & Bangert-Drowns (1990)	108	All the literature, but mostly college level	0.52	PSI, LFM

One might thus think that the difference is because the effects at college level are far higher and the 1990 paper didn't disaggregate. But no, the effect sizes for pre-college level in the 1990 paper are in line with the ~0.5 figure. The key bit here, and what Summaedu.org missed is that the studies in the 1983 meta are not necessarily mastery learning studies, they are "individualized systems of instruction":

Fifty-one studies met all the requirements that we established for inclusion in the meta-analysis. The first of these requirements was use of an individualized teaching system in the experimental class. Criteria for individualized systems included division of course content into chapter-length units, use of class time for individual work by students, and emphasis on formative testing. In most classes using individualized systems, students are free to move at different rates through course material and have to demonstrate mastery to advance from one unit to another, but we did not consider these absolute requirements for individualization. Our criteria for individualized systems were thus similar to those used by Hartley (1978) in her study of "individual learning packages."

So that's it? Not quite, because the paper also disaggregates studies by whether or not they had a mastery requirement, and the effect size found for studies (26 of them) using ML was found to be 0.05, so we get our mystery back, in an even stronger form.

The solution is in Kulik & Kulik (1989), there they state side by side that Bloom's LFM does have the expected half-sigma effect, while the Individual Learning Packages covered in the 1983 paper has a 0.1 effect. But why? The only plausible explanation is that there are major differences between the way IPI and PLAN work and the way PSI and LFM works, and that the effects from IPI/PLAN swamp those of PSI and LFM in the meta-analysis. Indeed, if we go to individual studies in the meta and look at those with negative effect sizes, those do not seem to be LFM/PSI. But then, what makes IPI so different? It does sound sufficiently close to what mastery learning is:

Individually Prescribed Instruction (IPI), developed at the University of Pittsburgh, was based on a “diagnostic-prescriptive” teaching cycle. The teacher used placement tests to assign each student to a particular unit in reading, Math, or science. Then the student worked independently with appropriate materials. The teacher assessed whether the student had attained mastery, assigning extra work if necessary.

Except that in IPI, when a student fails to progress, they re-study the same materials, while in LFM/PSI they get new materials, designed for students who failed the first time.

I couldn't find much work on IPI. But tentatively, it does seem like mastery learning works -only if- the remedial activities are sufficiently good.

Slavin's critique

Slavin's critique is not a meta-analysis, but what he calls "best-evidence synthesis". In the event that a research literature is full of shoddy papers, one has to go first through the work of throwing away studies that are not good enough to include in a meta-analysis, and this is what he does.

When reviewing what mastery learning is, he notes that mastery learning might indeed work because of longer exposure to the teaching material, but that this poses a dilemma for slower students: Maybe they would be better off covering more material in less depth than covering less material but fully mastering it. Teaching time is, after all, limited.

When looking at two studies that controlled for teaching time, if one looks at "learning per hour", mastery learning heavily (d=-1) underperformed regular instruction. Mastery learning, it might be, works better, but is less efficient than regular learning. In the case of Bloom's own work, the extra time allocated for remediation classes sums up to an extra day per week. So, Slavin argues, one should control for time spent learning, because what is doing the work here might just be exposure to the material, not anything specific to mastery learning., and not every study does this. Note that many ML proponents do also claim that even per unit of teaching , ML is more effective too.

Another issue is that of experimenters coming up with tests that target well what the ML students learn, but that matches less what the control group learns, thus biasing the evaluation. An example of this is a study from 1976 (Anderson, Scott, and Hutlock) that looked at effect sizes in Maths knowledge in grades 1-6 both at the end of the instructional period (d=.64) and three months later (d=.49). But then, when experimental and control groups were tested on an external mathematics test, not designed by the experiments, the effect size was negligible. Similarly in other study (Taylor, 1973) that looked at differences in "minimal essential skills" for algebra and "skills beyond essential" found that while for minimal skills the ML students did better, this was not so for those other skills, where they underperformed the control group. This study technically did not use ML as such (The amount of testing and corrective feedback sessions was limited to one per semester, ML demands a more fine-grained approach, at least once a month), but it is fair to bring it up when discussing the tradeoffs between learning a few basics well vs learning more advanced knowledge, but less well.

Then Slavin moves on to describe what criteria he will use to select valid studies; for example he will not consider studies that merely compare the results of a class in year 1 with the results of a new incoming class in year 2, taught with mastery learning: They are not the same students, and other things may have changed to alter the results. Second he discards studies that do not adjust for initial differences in skill in the control/experiment groups. Third, he discards studies that lasted less than 4 weeks. Fourth, he discard studies that less than two control groups and two experimental groups. This is to avoid effects from individual teachers or classes (Remember that most of these studies are not RCTs) .

Now, considering the actual evidence, he looks at various claims.

Mastery learning is better, adjusting for time spent. Students are better prepared even for concepts that are not explicitly tested in the periodic assessments.

Only 7 studies met Slavin's quality criteria (and most of these are randomised), finding indeed a median effect size of ~0, with the maximum being 0.25, and even that study had issues, he claims. Sample sizes here range from 6 classrooms the least, and 4 entire schools at most, covering Math and reading, in grades 1 to 9. The studies ran for between 5 weeks and a year. Note, this is for the claim "Given the same amount of instruction".

Mastery learning is better, adjusting for time spent. Students are better prepared, but only for those concepts explicitly tested in the periodic assessments.

Nine studies are deemed good enough, finding a median effect size of 0.255 (ranging from 0.18 to 0.27), but the studies are heterogeneous in design. One of the excluded studies is a rather large study undertaken in Chile, in that case the effect size was close to the median, but when breaking down in high/low performance students, it was found that the effect was larger for low performers (.58) and zero for high ability kids. Slavin excludes this study because the mean SES and IQ of the classes using mastery learning in that case was higher, and no adjustments were made for that. In the studies that measured retention (A few weeks or months after the last exam), most of them find insignificant differences between control and experiment.

In one of the studies that was included (Mevarech, 1986), done by a student of Bloom in Israel, the effect size for low ability kids (proxied by the fact that their parents did not go to high school) got close to the fabled two sigma (1.78); at the other end kids whose parents went to college also improved a lot, but not as much (0.66). Slavin then goes into why this was the case, he finds two possible issues: One was that while students were randomly assigned, teachers were not, and so it could be that some teachers were incredibly good, or others were incredibly bad. Another is that perhaps the teachers used mastery learning focused more on the specific concepts that would be in the test rather than teaching more general knowledge.

Mastery learning is better, if no adjustments for time spent are made

Four studies meet the criteria here, effect size of around zero, and same for longer term retention studies. There are of course a few studies that find larger effect sizes, which Slavin discusses.

Slavin concludes,

The best evidence from evaluations of practical applications of group-based mastery learning indicates that effects of these methods are moderately positive on experimenter-made achievement measures closely tied to the objectives taught in the mastery learning classes and are essentially nil on standardized achievement measures. These findings may be interpreted as supporting the "weak claim" that mastery learning can be an effective means of holding teachers and students to a specified set of instructional objectives, but do not support the "strong claim" that mastery learning is more effective than traditional instruction given equal time and achievement measures that assess coverage as well as mastery. Further, even this "curricular focus" claim is undermined by uncertainties about the degree to which control teachers were trying to achieve the same objectives as the mastery learning teachers and by a failure to show effects of mastery learning on retention measures.

These conclusions are radically different from those drawn by earlier reviewers and meta-analysts. Not only would a mean effect size across the 17 studies emphasized in this review come nowhere near the mean of around 1.0 claimed by Bloom (1984a, 1984b), Guskey and Gates (1985), Lysakowski and Walberg (1982), or Walberg (1984), but no single study reached this level. Only 2 of the 17 studies, both by the same author, had mean effect sizes in excess of the 0.52 mean estimated by Kulik et al. (1986) for precollege studies of mastery testing. How can this gross discrepancy be reconciled?

One, that Slavin is throwing away studies he deems of poor quality. In general, he is retaining about a quarter of the studies that are included in the meta-analysis discussed above. Another, Slavin is also including unpublished studies, on the grounds that those are less likely to suffer from publication bias. Also, Slavin explicitly corrected scores for initial ability, something the meta-analyses didn't do.

Slavin then goes into the theoretical reasons why, even when mastery learning sounds so compelling, it may not do much.

It may be that the teachers are not properly trained, or that the material used for corrective instruction is suboptimal. Indeed he points to some studies where these two issues were corrected, and they found a positive effect after a year of instruction; Mevarech also stressed (in a personal communication to Slavin) that the quality of this material is key. Or maybe those extra corrective lessons need even more time to be effective:

Studies of students' pace through individualized materials routinely find that the slowest students require 200-600% more time than the fastest students to complete the same amount of material (Arlin & Westbury, 1976; Carroll, 1963; Suppes, 1964), far more than what schools using mastery learning are likely to be able to provide for corrective instruction (Arlin, 1982).

Or, it could also be that feedback should be provided on a daily basis, not on weekly tests.

As to why mastery learning might work, Slavin thinks that a big part of why mastery learning may work in some cases is not holding students up to mastery and giving them remedial activities, but instead merely testing them and giving them feedback about what they don't know, and then moving on to the next lesson. In one study he cites where these two regimes were tested (teaching-evaluation-corrective and teaching-evaluation), both sets of students outperformed a control class that had less frequent tests, but they were not that different from each other, what is known as the testing effect.

On Bloom's two sigma problem, he finds issue with the framing itself:

The 2-sigma challenge (or 1-sigma claim) is misleading out of context and potentially damaging to educational research both within and outside of the mastery learning tradition, as it may lead researchers to belittle true, replicable, and generalizable achievement effects in the more realistic range of 20-50% of an individual-level standard deviation. For example, an educational intervention that produced a reliable gain of .33 each year could, if applied to lower class schools, wipe out the typical achievement gap between lower and middle-class children in 3 years—no small accomplishment. Yet the claims for huge effects made by Bloom and others could lead researchers who find effect sizes of "only" .33 to question the value of their methods.

And there's something to that: I'm doing a review of mastery learning instead of any other thing because of Bloom's claim of a large effect!

Replies to Slavin

Bloom himself (1987) replied that proper mastery learning under his LFM system has to involve students helping each other work through the corrective activities. Only one of the studies in Slavin's first claim examination meets Bloom's definition. On experimenter-made vs standardised test measures, he rather prefers the experimenter/teacher-made tests as they cover the exact intended objectives of the teaching. He gets quite emotional at the end(!)

It is a crime against mankind to deprive children of successful learning when it is possible for virtually all to learn to a high level.

Slavin (1987) reviews the critique above, and others, noting first that there are are only few points of agreement. They agree on the fact that LFM has no effects on standardised test performance, mastery learning effects are far less than 1 sigma in studies that last at least 4 weeks (Slavin would rather use a more stringent threshold), and mastery learning does need additional time of instruction to be effective (Bloom explicitly argues that this is needed for the method to work).

The points of disagreement lie in the validity of assessment by standardised tests. These tests cover more than what is necessarily taught in the mastery learning groups, and cannot be "overfitted" as easily by the mastery learning teachers, as they don't know the exact contents.

Later on, Slavin (1989) published an article, after having received the critiques cited above. As far as I know, there are no further replies to his comments. He goes over the comments that others (The Kuliks, Guskey, Bloom,...) of his review. Guskey went as far as implying that Slavin was deliberately trying to discredit mastery learning, even when, according to Slavin, he has no issue with it, and his (Slavin)'s own educational method - Success for All - is based on mastery learning too! The criterion that excluded most of the studies from the analysis was looking at longer-term (more than 1 month) studies, which doesn't seem unfair to me. After all, what killed the literature on cognitive gains at the pre-K level was also this fadeout effect over time.

And finally, in Mastery Learning Re-Reconsidered (Slavin, 1990) replies to the Kulik-Kulik-Bangert-Drowns reply mentioned above. Even after including newer studies, if one applies Slavin's methodological criteria to the more recent papers, the value in the Kulik et al. meta analysis would be the same as Slavin found.

However, the main issue of the effectiveness of mastery learning boils down to a question of values. The findings of positive effects of mastery learning on experimenter-made measures can be interpreted as supporting the view that this technique can help focus teachers on a given set of objectives. Educators who value this have a good rationale for using group-based mastery learning. However, the claim that mastery learning can accelerate achievement in general in elementary and secondary schools is still awaiting convincing evidence.

The Kulik, Kulk & Bangert-Drowns (1990) reply to Slavin I mentioned above is brief, saying that he did not consider other systems of mastery learning (Slavin looked at group-based (LFM) rather than individual-based (PSI) studies), and that he mostly focused on pre-college studies, while most LFM work is done at college level. The authors say they think Slavin does not disagree with them if one limits oneself to the literature examined by Slavin, with the exception of the inclusion on Slavin's paper of some studies that did not have a mastery treatment group(!), they claim. The authors refer us to Dunkelberger & Heikkinen, 1984 and Fuchs, Tindal & Fuchs, 1985). The authors then look at 11 studies that both themselves and Slavin consider good, and they find an effect size of around 0.36-0.45 in examiner-made tests, and 0.09 in standardised tests. Seems a good enough agreement.

They themselves admit:

Too few studies are available, however, for us to feel confident about these estimates of LFM effect sizes. We would therefore like to see more research on LFM effects, especially its effects on standardized tests.

Until more studies are conducted, researchers should keep in mind the current results: LFM students clearly do better than other students on tests developed to fit local curricula, and they do only slightly better than others on standardized tests that sample objectives from many school systems and many grade levels. There is no evidence to suggest that LFM has any negative effects on any type of student learning.

Finally, teachers and researchers can learn much more about mastery learning by looking at the full picture rather than the small corner of the research on which Slavin focuses. They can find more stable and reliable estimates of effect sizes in the larger literature on mastery learning. And they can learn about affective and behavioral outcomes of mastery learning; about the conditions under which mastery teaching has stronger and weaker effects; about the students in a classroom who are most affected by a switch to mastery methods; and so on. We believe LFM effects on precollege examinations constitute only a small part of the story.

Now, after reviewing this and having read the debate, what Guskey says in his review from 2015 sounds grossly unfair with Slavin's review:

A close inspection of this review shows, however, that it was conducted using techniques of questionable validity (Hiebert, 1987), employed capricious selection criteria (Kulik et al., 1990b), reported results in a biased manner (Bloom, 1987; Walberg, 1988), and drew conclusions not substantiated by the evidence presented (Guskey, 1987, 1988). Most importantly, three much more extensive and methodologically sound reviews published since (Guskey and Pigott, 1988; Kulik et al., 1990a; Miles, 2010) have verified mastery learning’s consistently positive impact on a broad range of student learning outcomes and, in one case (i.e., Kulik et al., 1990b), showed clearly the distorted nature of this earlier report.

If you want to keep reading more about the history of this literature, and the weaknesses of the earlier meta-analyses, section 2 of Evans (2018) is for you.

Sample sizes

What are the sample sizes in the Kulik meta-analysis? The paper itself doesn't say. But a study of group-based mastery learning by Guskey & Pigott (1988) does provide the sample sizes. Most of the studies have samples under 100; but the largest studies (~200 and ~400 students per group) still find large (0.5 and 1 for the largest) effects. (The larges of them is the Cabezon study in Chile I discussed above). The authors note the low quality and heterogeneity of the literature.

Another factor that may contribute to variation in the magnitude of the effects is lack of precision in specifying the treatment or the fidelity of the treatment.

Much confusion exists about what actually constitutes mastery learning, and survey data indicate there is great variability in programs labeled "mastery learning" (Jones, Rowman, & Burns, 1986). Without detailed information about the instructional format, the characteristics of the feedback and corrective activities offered to students, and the specific procedures used to evaluate student learning, it is difficult to judge how closely an intervention replicates the ideas of Bloom (1968). Many studies also failed to describe adequately the conditions of the non-mastery control group. The diverse nature of the programs and treatments considered in these studies undoubtedly contributes to the variation in study effects.

A substantial chunk of this literature is also PhD thesis, and conference papers. That's not necessarily a bad thing, but it's an interesting curiosity; I've never went into a literature that looked like this!

Newer studies

All these metas are looking at old studies, we can look at some of the new work to see if the effects persist.

Jerrim et al. (2015) studied a mastery program for mathematics for Year 7 (Equivalent to grade 7) in London, with a sample of over 5000 students. No significant effects were found (d=.06), and this was an RCT. But then, this trial did not test the same thing the old studies were testing:

It is important to note that the Mathematics Mastery programme differs from some examples of mastery learning previously studied. For example, a key feature of many apparently effective programmes studied to date was that once pupils have completed each block of content they must demonstrate a high level of success on a test, typically at about the 80% level. Pupils not meeting this target would receive additional instruction, while those who succeeded would engage in enrichment activity that sought to deepen their understanding of the same topic. This is a different approach to that adopted by the Mathematics Mastery programme, within which the developers sought to provide all pupils with “opportunities to deepen understanding through enrichment throughout their time studying the content”.

In Mathematics Mastery, the class spent longer than usual on each concept or procedure the first time they studied it, but they did not significantly delay the starting of new topics in the event that some pupils were still unable to achieve mastery. Rather, the intention was that the majority would achieve a good understanding of the key ideas in the required time, and that intervention would be provided for any pupils at risk of falling behind.

Vignoles et al. (2015) got similar results, when looking at Year 1/Kindergarten, as part of the same study.

Kalia (2005) did a far smaller study in India, with only 30 students per group (90 total), testing a baseline vs mastery learning vs other learning approach. An effect size of 1.64 was found. It does not strike me as a solid study.

Miles (2010) in his doctoral dissertation found a d=0.53 effect, but again on a small sample (43 and 36 students in the control vs treatment group). I couldn't access the original work for this review.

The evidence for tutoring (and software tutoring)

After we have looked into mastery learning, we may as well look into tutoring. After all, it is what in Bloom's study got the best results.

The first thing to note here is that the tutored students in Bloom's Two Sigma paper were not just tutored, they were tutored to help them follow mastery learning. And not only that, according to VanLehn (2011), the standards to which the students were held varied: tutored students were held to higher standards. VanLehn more broadly looks at the relative efficacy of two kinds of computer aided systems, and human tutoring, relative to no tutoring at all.

One might posit that tutoring works because the tutors are able to gauge how competent students are, what their weaknesses are; and in general form a model of how the student learns so that they can be better guided in their study. But VanLehn is sceptical that this is the reason⁴:

Although human tutors usually know which correct knowledge components their tutees had not yet mastered, the tutors rarely know about their tutees’ misconceptions, false beliefs, and buggy skills (M. T. H. Chi, Siler, & Jeong, 2004; Jeong, Siler, Chi, 1997; Putnam, 1987). Moreover, human tutors rarely ask questions that could diagnose specific student misconceptions (McArthur, Stasz, & Zmuidzinas, 1990; Putnam, 1987).

When human tutors were given mastery/nonmastery information about their tutees, their behavior changed, and they may become more effective (Wittwer, Nuckles, Landmann, & Renkl, 2010). However, they do not change their behavior or become more effective when they are given detailed diagnostic information about their tutee’s misconceptions, bugs, and false beliefs (Sleeman, Kelly, Martinak, Ward, & Moore, 1989).

Moreover, in one study, when human tutors simply worked with the same student for an extended period and could thus diagnosis their tutee’s strengths, weaknesses, preferences, and so on, they were not more effective than when they rotated among tutees and thus never had much familiarity with their tutees (Siler, 2004). In short, human tutors do not seem to infer an assessment of their tutee that includes misconceptions, bugs, or false beliefs, nor do they seem to be able to use such an assessment when it is given to them

Is this representative of the best tutoring can do? Hardly.

VanLehn looks at other possibilities: Maybe tutors use sophisticated teaching techniques; maybe they select tasks in an highly individual way for each student, maybe they are able to enrich their explanations with general domain knowledge, maybe tutors act as a motivational aid, but he found they typically don't, or when they do, they don't have an effect on the desired outcome that is being measured).

What he finds plausible as an explanation is that

1. Tutors give feedback when student make mistakes, asking students to explain why they do what they do, and spotting the misguided assumptions or concepts.
2. Tutors guide students reasoning by asking them relevant questions about what they currently think. VanLehn gives a brief example of a student answering "What falls faster, a golf ball, or a feather, in vacuum"; the student gives the right answer, but a subpar reason (The student saw a video of it), and the teacher accepts the answer, but asks why, eventually leading the student to a better explanation. Unlike feedback, this is meant to be proactive.
3. Tutors regulate the frequency of student behaviours; nudging them to be more active or interactive in the ways they learn; in turn by hypothesis these kinds of activities support better learning. For example, a student might just sit on a lecture; a tutor might encourage the student to take notes, read more about the subject being discussed, or ask questions when they don't understand.

VanLehn then looks at a few (low-sample size) cases (teaching cardiovascular physiology to medical students, or basic physics), where students without tutoring were compared with students tutored by software and tutored by human tutors: Tutoring is shown to be highly effective, but human tutoring did not prove to be superior to the software-based approach.

Then he looks at the broader literature. The average effect from tutoring seems⁵ to be only d=0.79, (This is not quite 2-sigma, but it is a HUGE effect nonetheless); a similar effect was found for good quality software based tutors. What makes software good quality is that it is able to provide feedback at a very granular and concrete level, but after a certain point, he finds, there is a plateau and more finer-grain explanation do not improve learning.

VanLehn is aware this is not quite what Bloom found, so he looks into possible reasons as to why. Could it be that tutoring expertise makes another sigma difference? No, studies don't find substantial effects from tutoring expertise. He then looks at the two studies that found the two sigma gains and why that might have been. The tutors in those studies were not particularly skilled, and as mentioned at the start of this section, the tutored students were tutored using a particularly strict version of mastery learning.

Another study he looks at was later on replicated, but the replication found a smaller (d=0.52) effect size. The next largest effect size found in the literature is 0.82. Most of these studies are fairly small sample size, so high variance is to be expected. Also, he notes that the studies may not be representative of all tutors. Maybe there are really good tutors out there that are not being measured here. Also, going meta, VanLehn speculates that the reason human tutoring was not found to be better than good software assisted tutoring is that regular tutors do not practice their skills deliberately, they don't get much feedback from their students over time.

Bloom’s d = 2.0 effect size seems to be due mostly to holding the tutees to a higher standard of mastery. That is, the tutees had to score 90% on a mastery exam before being allowed to continue to the next unit, whereas students in the mastery learning classroom condition had to score 80% on the same exam, and students in the classroom control took the exams but always went on to the next unit regardless of their scores. So the Bloom (1984) article is, as Bloom intended it to be, a demonstration of the power of mastery learning rather than a demonstration of the effectiveness of human tutoring.

More recent work (Ma et al., 2014) has also found that this overall result: tutoring is as good as software-based approaches; if anything the effect sizes are smaller (g=0.4)⁶, and there seem to be no publication bias. Focusing on a particular field, computer science, Nesbit et al. (2014) find large effects of software tutoring (d=0.67) relative to regular classrooms. Note that they also find an even larger effect for good quality software tutoring vs very basic computer based instruction (d=0.89). Coursera would be an example of a very basic system in this typology. Other meta-analysis( Steenbergen-Hu & Cooper, 2014 ) focusing on college students have found that human tutors do outperform, contrary to VanLehn, but when disaggregating by software quality (what they dub substep vs step-based tutoring), the findings are again coherent with VanLehn.

Another meta-analysis, Kulik & Fletcher (2017) targets mostly students above grade 6 (Fletcher, 2018), showing that even for older students and more complex subjects there are still gains from using software tutors. In fact, the effects from software tutoring are markedly larger for post-secondary instruction compared to elementary and secondary levels (Effect sizes 0.44 vs 0.75). Fletcher also stresses that for simpler learning scenarios, as those found in pre-university education, "drill and practice " systems like DI work fine, at a lower cost.

The one case so far where there seems to be a larger effect is in the DARPA Digital Tutor case; developed to train US Navy information system technicians. A 16 week software based course was compared to 35 weeks of a regular classroom course. Effect sizes ranges from 1.97 to 3.18(!) in the two evaluations reported in Kulik's meta-analysis. The students even outperformed the instructors!

DARPA's study

This section is a summary of the following reports: Fletcher & Morrison (2012), andFletcher & Morrison (2014) .

In 2010 there were two trials of DARPA's sponsored Digital Tutor (DT) for the Navy, in April (4 weeks of DT training) and in November (8 weeks), overseen by an external party, the Institute for Defense Analyses (IDA). The design was an RCT, where they also measured IQ (AFQT) in the control and experimental groups to make sure they were roughly similar (And they were)

• In the April trial, the assessment was a written knowledge test, where the DT students (20) outperformed regularly taught students (18) (the regular course goes on for 10 weeks, d=2.81) and also the instructors (13) of the regular course (d=1.25). (Numbers in bracket indicate the sample size for each group). The test questions were in part provided by the DT developer (93 items), the instructors (51 preexisting questions+25 new ones), and IDA (5). Before administering the test, it was judged by four IT support staff from IDA as a good measure of IT admin knowledge.
• In the November trial they had four groups: students taught for 7 weeks with DT (20), one regularly taught group (18) as before, one group (20) taught for ~10 weeks in a different but related course, IT of the Future( IToF) and the instructors for the regular course(10). As before, they used a written test, but they also included a practical examination, and an oral exam for a third of randomly selected DT and IToF students. Again, DT students outscored everyone else: the instructors (d=1.35) in the knowledge test, the IToF students in the practical exam (d=1.9), the regular students in the written test (d=4.68), and the oral reviews (d=1.34).

With effect sizes this large, measured in so many different ways, maybe DARPA has solved Bloom's two sigma already! Also, unlike with mastery learning, the DT students were taught in less than half the time as everyone else! One can surely argue that the larger effects in the knowledge tests were due to the fact that a lot of the questions were provided by the DT developer, and the same was the case for the practical examinations. But it was not the case for the oral examinations, and even then the tests were externally reviewed and considered fair, so while we can assume a part of those large effect sizes are due to a better fit between the test and what was taught with DT, there still seems to be a legitimate improvement.

One might argue that we should disregard the low sample size study here, but I argue that we should take it seriously. First, if one expects an effect of d=1, and one wants a statistical power of 80%, the sample size is about 17 subjects per group, around what DARPA had. Second, it was not just one test, but a few, all showing large effects. Third, there were three trials (The test run in 2009 and the full runs in 2010), and all results were reported. And fourth, each trial is composed of many questions, over a hundred in the case of the knowledge test, one can get lucky in one, but that's far less likely in a comprehensive assessment.

Given the results, there was a next stage test with a 16 week DT course compared to a 35 week course, and to another group of skilled (9 years of experience on average) technicians. Again the samples were small, but the effect sizes are still there: DT students outperformed the technicians (d=0.85) and regular students (remember, they studied for twice the time!) (d=1.13) in practical tests, and similar magnitudes were observed for the oral examinations.

All in all, this is really good evidence for the possibilities of software-based tutoring; as they not only tested theoretical skill, but also applied knowledge, in a varied number of ways.

Making good software for tutoring is hard

A common theme in the studies cited above is comparing advanced vs simplistic computer based tutoring. Making good software tutors is hard, and it would be a long review of its own to properly look at tutoring software⁷.

Here's a review (Alkhatlan & Kalita, 2018) of how ITS's look like from a design point of view. The authors also mention that the best human tutors outperform the best software. I would be surprised if this were not the case. This adds some nuance to VanLehn's review: Yes it may be that the average tutor performs on par with the average of the best software, but the best of tutors perform even beyond what software can do. It's easy to imagine, as a star tutor could also easily assign students a software tutor, and supplement that with other activities.

Andy Matuschak (personal communication) suggested that the key difficulty is that one needs both to be a good creative problem solver, and have domain knowledge in order to translate knowledge and explanations into good software. Many are developed by PhD students and then abandoned. Even the DARPA tutor doesn't seem to have been put into production yet, for some reason.

Looking at other fields

Having completed the review of the core topics of this essay, it is worth looking at other fields that are related but seem to be in a better shape in terms of evidence behind them to see what should we expect. After all, if we knew that no other educational intervention has an effect size above 0.1, it would be unlikely that the ones under consideration are all that special. In effect, this section tries to put what I've already discussed in context.

The reliability of educational research in general

Knowing the state of the educational research field in general gives us some prior expectation for what would happen if we had proper large sample RCTs for the methods being examined. If we knew nothing about ML, we should expect it to have a very small positive effect, as this is the average effect found by Hugues & Matthew (2019), who argue that most large scale educational RCTs are often uninformative

What does uninformative mean here? The authors dub a study uninformative if its findings are consistent with the associated intervention being either effective or ineffective. Whether or not an RCT is informative in these terms therefore depends upon both its effect size and the precision with which that effect size is estimated.

They review 190 RCTs they deem to be high quality conducted prior June 2018 that targeted K-12 students and measured some quantitative metric of academic nature (e.g. test scores). The average effect size is 0.06 and highly heterogeneous, but there is no sub-analysis that reveals particularly stronger effects on average; also the confidence intervals were large. When an effect size is, say, 0.06 +/- 0.3, what is one to think?

The authors consider that this result, finding an effect size smaller than those found in individual studies for the different methods may be due to an unreliable literature, the interventions being legitimately ineffective, or the interventions being poorly designed so that they can't detect a hypothetical true effect: the educational methods being deployed could not be as good as the ones tested in labs. As with most research, the authors conclude that there should be more research into explaining why this is the case.

In this work, the Jerrim et al. (2015) paper I discussed above was mentioned, and it is the closest to what concerns us in the present literature review; the others do not seem to be either about direct instruction or mastery learning.

What works, according to this large review of RCTs? I provide below the effect sizes, evidence quality assessments and Bayes Factors for the top interventions.⁸

• "Improving Writing Quality", aimed at improving the writing skills of struggling students, involving providing kids with guidelines of what good writing looks like and how they should approach the process of writing (d=.74, strength of evidence judged as 2/5,Bayes Factor(BF)=10.52)
• "Butterfly Phonics", aimed at improving the reading skills of struggling students, which involves small (6-8 students) groups, and constant feedback through the class. (d=.43, strength of evidence judged as 0/5, BF=3.6)
• "Access to Algebra I", aimed at improving performance in algebra in grade 8 at-risk students, using a web-based course (d=.4), BF=154
• "One to one coaching", aimed at improving reading and writing skills of kids with low levels of attainment in English (d=.36, strength of evidence judged as 3/5, BF=4587)

These target students that are at risk, as with the Direct Instruction literature, and the effect sizes are around what the DI literature also finds, if we take it at face value.

Cheung & Slavin (2016) studied what features of studies correlate with effect size, in general. The two largest factors influencing the results are sample size, and the kind of test that is used to measure performance:

• Sample size: Low sample size (<100) studies find an average effect of .38, large samples (>2000) find .11
• Measurement type: Studies using measures designed by the experimenters find larger effect sizes (0.4) compared to studies using independent measures (0.2)
• Design: Randomized studies find an effect of 0.16 on average, quasirandomized studies find 0.23 on average.
• Publication status: Published studies find an effect of 0.3, unpublished studies find .16.

The possibility of improvement through deliberate practice

Deliberate practice -or practising something "properly" for extended periods of time - is also a related field that we can look at to better understand what expectations should we have for tutoring and mastery learning.

The most recent meta-analysis of deliberate practice and its impact on a range of fields (Macnamara et al., 2014) indicates that, relative to games, music or sports, where practice is somewhat associated with better performance (18-26% of variance explained), in education this number falls to 4%. A later meta-analysis looking at sports exclusively finds similar results (Macnamara et al., 2016). When looking only at professional athletes, cumulative deliberate practice explains only 1% of the variance in performance, presumably because there are decreasing marginal gains to deliberate practice and at that point, genetic endowments is what differentiates those elite athletes. If everyone is training hard, there are only so many hours in a day one can train for. There was also no correlation between the age at which athletes started training and performance. For internally paced (darts) vs externally paced (volleyball) sports, deliberate practice seems to work substantially better for the former (41% of variance explained), which makes sense to me, as there is less randomness, but did not reach significance in the meta-analysis (p=0.08).

in a study of field hockey players included in the present meta-analysis, Güllich (2014) found a nonsignificant difference in accumulated deliberate practice hours between Olympic gold medallists (M = 3,556, SD = 1,134) and field hockey players who played in the first four divisions for their country but who had not achieved international success (M = 4,118, SD = 807). Similarly, in a study of swimmers included in the present meta-analysis, Johnson, Tenenbaum, and Edmonds (2006) found a nonsignificant difference in accumulated deliberate practice hours between highly accomplished swimmers (M = 7,129, SD = 2,604) and swimmers who had not yet achieved similar accomplishments (M = 7,819, SD = 2,209).

What about chess? Are Grandmasters good because they practice or because they were born with skills that are well suited for chess? At least for the case of intelligence, the correlation doesn't seem to go beyond r=0.35 in a meta-analysis of amateur and skilled players with ELOs between 1311 and 2607 (Burgoyne et al., 2016), this implies a variance explained (R^2) of around 6%. If we look only at professionals, the correlation is smaller, 0.14 This does not mean the other 94% is explained by practice. Indeed, if we look at heritability more broadly, for chess skill it may be around 48% (Vinkhuyzen et al., 2009 ) .

What's the impact, then, of deliberate practice? There is one paper (Burgoyne & Nye, 2019) that looks at it in a sample of moderately to highly skilled chess players (ELOs between 1150 to 2650) and we get that it accounts for 34%. Note that this doesn't mean that deliberate practice doesn't matter for novices! Indeed, for novices practice is almost all there is. Higher intelligence or better memory may give players the ability to better evaluate a board, but practice gives players the ability to do a such evaluations to begin with! It is only when one has moved past the novice stage when the effects from innate skills will begin to appear.

Ericsson (2016) who does think that deliberate practice matter greatly thinks that Macnamara et al. overreached in their definition of deliberate practice; Ericsson argues that only a very special kind of practice should count, concretely practice that has been designed and/or implemented with the help of, a coach or teacher.

One on one coaching for national and international-level athletes is suggested by Ericsson as one clear example: He says there is a high (>0.8) correlation between time spent with a coach and performance; the studies he bases his estimates off were not in the Macnamara et al. meta-analysis. Also, Macnamara et al.'s counted as valid subjective measures of performance, while Ericsson would rather have purely objective measures. Ericsson goes as far as claiming that no genes have been identified that account for differences in individual performance, something which is clearly false, especially for intellectually demanding tasks. Even if no genes were identified, the fact that heritability of sport performance is far from negligible suggests that there is a strong case for a genetic basis for achievement, even when concrete genes cannot be identified yet.

Macnamara et al. (2016) reply to Ericsson that first, he himself has used non-objective measures in his studies on deliberate practice, and that second, in his work he hasn't restricted his definition of deliberate practice to the narrow definition Ericsson wants them to use. Even then, Macnamara et al. did look at a breakdown by measure type, and indeed objective measures do show a somewhat stronger effect from deliberate practice, but still under 25% of total variance explained in performance.

Finally, in a broader look at the literatures on cognitive performance improvement (They look at grit, growth mindset, brain training, deliberate practice, and bilingualism) Moreau, Macnamara & Hambrick (2018) find no evidence that these practices do anything to improve performance, in any way defined, except for deliberate practice, that does improves individual performance in some cases, but that it does not explain large differences found between individuals at a professional level.

The possibility of improvement through spaced repetition

If the above seems a bit pessimistic, saying that practice doesn't matter, the literature on spaced repetition says the opposite. As reviewed by Gwern⁹, the effect size of spaced learning vs massed learning (or cramming) is d=0.42 (Or perhaps a bit less), and has been found across a range of domains. Note that this is not an effect size of spaced repetition vs not studying again at all. If we asked someone to memorize a set of new, hard to remember, facts in a week, and someone else to use spaced repetition to keep that fresh over a year, at the end of that year, the effect size would be massive, as the first person may as well have forgotten it all while the second has kept it fresh.

Why would mastery learning work? Some proposed experiments

Suppose that something by the name "The Incredible Learning Method" or TILM has been shown to increase performance by d=0.5. One then wonders what TILM is. TILM consists on doing spaced repetition and doing pushups every day.

Should we then recommend that kids do pushups if they want to learn? Or should we find what, ultimately, causes TILM to work?

In this approach, we break down a method into its components and experiment with them separately, or together by parts, seeing what effects we find. Then, we could try to study how each of the subcomponents behaves in other samples, or try to find neuroscience-level explanations for them.

For spaced repetition, the answer here would be the underlying idea of there being a forgetting curve which in turn might be possible to explain by some feature of how the brain works at a low level.

In fact, could it be that mastery learning is spaced repetition in disguise?

Or, it could also be that the thing doing the trick is just more time: If we assume that the more exposed one is to a concept more one learns it (with perhaps some plateau at the end), then the fact that a student keeps studying over and over the same material would increase performance. If so, mastery learning wouldn't have an effect if one controls for time invested in instruction. As Slavin puts it:

In an extreme form, the central contentions of mastery learning theory are almost tautologically true. If we establish a reasonable set of learning objectives and demand that every student achieve them at a high level regardless of how long that takes, then it is virtually certain that all students will ultimately achieve that criterion.

Or, it could also be that it is just the testing that is doing the work. Recall, mastery learning is a study-test-feedback-corrective loop. Slavin found that the study-test-feedback loop works almost as well. But we also know that study-test also works! This is known as the testing effect.

Or, it could also be that mastering lesson N does have an impact on better absorbing the knowledge in lessons N+i. If so, a way to study this would be teaching a group with mastery learning and another with regular methods one lesson, then teaching both groups with regular methods lesson 2. If mastery learning works, then the group of students that originally was taught with mastery learning should get better results. This is, it seems to me, the only genuine "mastery" effect.

Conclusion

Bloom noted that mastery learning had an effect size of around 1 (one sigma); while tutoring leads to d=2. This is mostly an outlier case.

Nonetheless, Bloom was on to something: Tutoring and mastery learning do have a degree of experimental support, and fortunately it seems that carefully designed software systems can completely replace the instructional side of traditional teaching, achieving better results, on par with one to one tutoring. However, designing them is a hard endeavour, and there is a motivational component of teachers that may not be as easily replicable purely by software.

Overall, it's good news that the effects are present for younger and older students, and across subjects, but the effect sizes of tutoring, mastery learning or DI are not as good as they would seem from Bloom's paper. That said, it is true that tutoring does have large effect sizes, and that properly designed software does as well. The DARPA case study shows what is possible with software tutoring, in the case the effect sizes went even beyond Bloom's paper.

Also, other approaches to education also have shown large effect sizes, and so one shouldn't privilege DI/ML here. The principles behind DI/ML (clarity in what is taught, constant testing, feedback, remediation) are sound, and they do seem more clearly effective for disadvantaged children, so for them they are worth trying. For gifted children, or in general intelligent individuals, the principles of the approaches do still make sense, but how much of an effect do they have? In this review I have not looked at this question, but suffice to say that I haven't found numerous mentions of work targeting the gifted.

That aside, if what one has in mind is raising the average societal skill-level by improving education, that's a different matter, and that's where the evidence from the DI literature is less compelling. The effects that do seem to emerge are weaker, perhaps of a quarter of a standard deviation at best. ML does fare better in the general student population, and for college students too.

As for the effect of diverse variables on the effects, studies tend to find that the effects of DI/ML fade over time -but don't fully disappear-, that less skilled students benefit more than highly capable ones, and the effects vary greatly on what is being tested. Mastery learning, it seems, works by overfitting to a test, and the chances that those skills do not generalise are nontrivial. As in Direct Instruction, if what is desired is mastery of a few key core concepts, especially with children with learning disabilities, it may be well suited for them. But it is yet unclear if DI are useful for average kids. For high SES kids, it seems unlikely that they would benefit.

The history of the educational research literature is one plagued with low quality small sample size studies that were done decades ago, with less work being done now. It can be that now researchers are focusing on studying other instructional methods. Still, the fact that most large RCTs tend to find little effects should make us have a sceptical prior when presented with a new educational method.

Coda: What should you learn?

I have been discussing above learning methods. But what about learning content? What should one learn? Bryan Caplan, in his book The Case Against Education¹⁰ argues that skills are not very transferable: you get good at what you do, and you quickly forget everything else. This informed my priors when looking at the mastery learning literature; and so I was not that surprised to find the issue with the kinds of tests I outlined in my section on Slavin.

Caplan is right, and this opens an avenue to improve teaching: Suppose you focus on the very basics that will most likely be useful to the students in the future (reading, writing, mathematics). With the time freed up from not teaching other subjects, one can both help disadvantaged students get good at those core topics, and let non-disadvantaged students use the extra time to learn about whatever they want. I would even suggest let them go home, but it may be argued one of the implicit roles of school is that of a place to keep the kids while the parents are working, a kindergarten for older children, but if parents are okay letting their kids roam around, and cities are safe, this is not an issue. Definitely worth exploring.

Granting that one can use DI to hammer down very basic points, should one also hammer down History and English Literature? Just because you can make the learning of those happen doesn't mean that you should: the effectiveness of an intervention also depends on the values being used to judge it. What's the effect size of removing History from the curriculum and leaving more time for the kids to play?

Questions

1. Why aren't these methods more commonplace? I can understand that tutoring is expensive, but developing high quality software for tutoring is a one-off expenditure. Especially for large-scale public systems, it should be easy for them to fund it. Mastery learning doesn't seem that expensive to implement either. A place to start, for the case of Direct Instruction, is McCullen & Madelaine (2014)
2. How much do teachers matter, as an overall question, without focusing on particular methodologies. SSC says not much. Indeed, some recent work suggests that students are almost as good professors as professors themselves in a university setting (Feld et al., 2019)
3. How well does grouping students by ability (tracking/ability grouping) work. Again, SSC
4. Slavin has his own preferred educational approach, Success for All. Does this work? The effect sizes reported for this seem to be around 0.25, and studies comparing it to DI find similar effects. In fact, DI and ML are explicitly components of SfA, as per Slavin himself. If anything the evidence seems better than that of DI, and the effect sizes are more credible.
5. Digging deeper into the specifics of tutoring software
6. Pre-university takes a lot of time, over a decade. Can this be compressed in a year?
7. What about education for adults? There is a market of education out there for those in the need of various skills (e.g. language). What are the predominant approaches? Do they work?
8. Digging deeper into the specifics of tutoring

Changelog

• 2019/08/01 Fixing typos, improving style
• 2019/08/02 Clarify Direct Instruction vs direct instruction
• 2019/08/03 Add question on tutoring
• 2020/06/21 The RCT for Khan Academy was published, shows no effect. Thanks to Pablo Repetto for pointing this out.
• 2020/09/10: Success for All may not be as good as I originally said, a large RCT from 2015 that was cited by SfA actually does either show small effects, or nonsignificant effects.
• 2020/09/15: Typos. Thanks to Ivan Savov
• 2021/04/22: Fix section numbers

Acknowledgements

Thanks to Gwern, Andy Matuschak, Jaime Sevilla, Alex Tabarrok, Tyler Cowen, Tom Higgins, @Ed_Realist, and Stephen Malina for their valuable comments.