Análisis del Brayton Ready Engine
En el trabajo anterior [1] se presentó el Brayton Ready Engine, describiendo su funcionamiento y algunas características del motor. En este trabajo se realizarán algunos cálculos para conocer más en profundidad el comportamiento del aparato. Dadas las limitada cantidad de información disponible, se han hecho suposiciones razonables allí donde faltasen datos.
Se presenta en primer lugar una tabla con datos obtenidos directamente de la bibliografía
| Proporción aire/combustible | 12:1 (en volumen) | | Combustible | _Coal gas[[1]] | | Volumen del depósito | 0.63 L | | Presión del depósito | 4.1 bares | | Volumen del cilindro A | Mitad que el depósito | | Potencia para motor | 4 hp (3kW) a 180 rpm (modelo de 1878) | | Eficiencia | 17% | | Consumo de combustible | 32 pies cúbicos por caballo por hora | | Relación de calores específicos [2] | 1.35 |
Una primera operación es estimar las características del combustible del motor. Para ello, se parte de la composición del mismo [3] y se realizan ciertas operaciones elementales para obtener la siguiente tabla:
| Compuesto | % en volumen | ** (kJ/l)** | Masa molecular (g/mol) | % en masa | | Hidrógeno | 50 | 10.05 | 2 | 12.34 | | Metano | 35 | 36.4 | 16 | 58.45 | | Monóxido de carbono | 10 | 12.63 | 28 | 29.19 | | Otros | 5 | - | - | - |
Asimismo, para estimaciones de volúmenes por mol, se asumirán condiciones normales a 1 atm y 273 K, por tanto 1 mol serán 22.4 litros.
El cálculo de la entalpía de combustión ** **del combustible puede aproximarse ponderando las entalpías de combustión por unidad de volumen de cada componente por el porcentaje volumétrico de casa una. 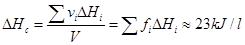 Resulta superior al de la bibliografía de 20.5 kJ/l y se tomará el inferior.
Resulta superior al de la bibliografía de 20.5 kJ/l y se tomará el inferior.
Además, puede calcularse la densidad del combustible. Por comodidad, se calculará la masa de 1 litro. Si se asumen 100 l del gas, se tendrán 59 l de hidrógeno, 35 l de metano y 10 l de monóxido de carbono, es decir 2.64 moles de hidrógeno , 1.5625 moles de metano y 0.446 moles de monóxido asumiendo. Esto hace un peso total para los 100 litros de 42.768 gramos. Por tanto la masa por litro será de 0.43 gramos. Puede calcularse también la energía específica del combustible: .
Las reacciones de combustión que se producen en el combustible, asumiendo combustión estequiométrica son
Aplicando fórmulas deducidas de las expresiones anteriores puede calcularse el dosado estequiométrico, el dosado absoluto y el dosado relativo. Si entran 100 litros de combustible, entrará 16 veces en volumen esa cantidad de aire, que en masa son 1554 gramos.
Por tanto, se produce combustión con mezcla pobre, lo que llevará a una mayor cantidad de NOx en el escape.
Puede estimarse la temperatura de combustión del combustible e partir de su temperatura adiabática de llama, que por simplificar se calculará ponderando por masa las temperaturas adiabáticas de llama de cada uno de los componentes [4] , resultando 2376 ºC. Como la mezcla no es estequiométrica, será inferior. Se asume que lo es en 0.7 veces, a la vista de los gráficos de variación de esta variable recogidos en [5]. De modo que finalmente se tomará 1663.2 ºC, o 1936.35 K. El rendimiento de Carnot del motor podría entonces estimarse en
Pero siendo un ciclo Brayton, su rendimiento ideal será inferior incluso asumiendo expansiones y compresiones isentrópicas:
Finalmente pueden calcularse las emisiones de CO2 del motor partiendo de las ecuaciones de combustión vistas antes .
El consumo por kWh puede calcularse a partir del consumo por caballo-hora:
Y las emisiones específicas son entonces
Esto es razonable porque si bien el motor es ineficiente, su combustible está formado principalmente por hidrógeno y metano y su fracción másica de carbono es por tanto reducida. Por último, puede realizarse un segundo cálculo de la eficiencia del motor. Primero se calculan los kilojulios efectivos que se obtienen por kilogramo de combustible
Si se quema 1 kg de combustible por segundo, el rendimiento interno es
Que se aproxima al rendimiento encontrado en la bibliografía. Al final, se han obtenido los siguientes datos:
| Parámetro | Valor | | Rendimiento de Carnot | 85% | | Rendimiento del ciclo Brayton | 31% | | Rendimiento interno real del motor | 15% | | Dosado relativo | 0.67 | | Emisiones de CO2en kg por kWh | 1.043 |
Figura 1: Medidas del Brayton Ready Engine. (En píxeles. 37 pix=1 pulgadas)
Bibliografía
| [1] | El Blog de Artir, "El Brayton Ready Engine, la primera ‘turbina de gas’," ETSII, 2014. | | [2] | Roy Beardmore. RoyMech. [Online]. http://www.roymech.co.uk/Related/Thermos/Thermos_Specific_heat.html | | [3] | Bryan G. Reuben, Jeffery S. Plotkin Harold A. Wittcoff, Industrial Organic Chemicals. | | [4] | The Engineering Toolbox. The Engineering Toolbox. [Online]. http://www.engineeringtoolbox.com/flame-temperatures-gases-d_422.html | | [5] | A. Makino, T.F. Lu C.K. Law, "On the Off-Stoichometric Peaking of Adiabatic Flame Temperature," Princeton Univesrity, JAXA, 2006. | | [6] | Marty W. Irwin Brian H. Bowen. (2007, Agosto) Purdue University. [Online]. http://www.purdue.edu/discoverypark/energy/assets/pdfs/cctr/outreach/Basics3-CTG-CTL-Aug07.pdf |
[[1]] Por la bibliografía, se sabe que la primera versión del motor usaba gas. Teniendo en cuenta la época en la que se encuadra este motor, suponemos que es Coal gas, similar al que se usaba en iluminación de farolas hasta la entrada de la electricidad a principios del s. XX de la mano de inventores e industriales como Tesla, Edison o Westinghouse. El coal gas se obtenía por pirólisis del carbón y estaba compuesto de hidrógeno, metano, dióxido de carbono y monóxido de carbono. Su combustión libera unos 20.5 kJ por litro [6]


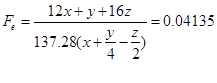

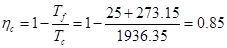
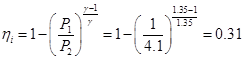
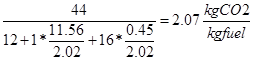

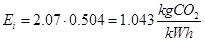
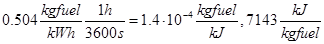
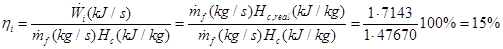

Comments